奇异值分解–深度学习的数学基础

1. 概述
2. 奇异值分解
3. 特征值与特征向量
4. 小结
5. 补充说明
附录1 二维空间的正交变换
附录2 三维空间的正交变换

在 $ \text{Attention} $ 机制（或 $ \text{Multi-Head Attention} $ ）中我们会看到这样的变换：$ \text{Attention} = softmax(\frac{Q_iK_i^{T}}{\sqrt{d}}) $，其中这里 $ Q_i = XW_i^Q $ 那么如何理解这里的 $ XW_i^Q $ 呢？该变换是向量空间内一个典型的线性变换，而这里的 $ W_i^Q $ 就是对应的线性变换矩阵，在早期 GPT 模型中该矩阵是一个$ 768 \times 64$ 的矩阵，研究该矩阵的典型方法就可以使用 $ \text{SVD} $ 分解，本文展示了简单的二维空间中 $ \text{SVD} $ 分解以及对应的几何意义，从而可以较好的帮助理解上述计算的深层次含义。

关于奇异值分解（$ \text{SVD} $）能够解决的问题这里不再详述。本文通过展示对于平面空间中的线性变换进行奇异值分解，从而观察该分解如何通过“几何”的方式描述一个线性变换，从而建立对线性变换的直观理解。本文的示例是一个$ 2 \times 2$的矩阵，所以还补充了对该矩阵的特征值/特征向量的计算，从而对比这两种方法在处理“方阵”时的异同。

1. 概述

本文通过对二维空间中的一个线性变换（满秩方阵） $ A = \begin{bmatrix} 1 & 2 \\ 2 & 1 \end{bmatrix} $ 进行 $ \text{SVD} $ 分析、特征值/特征向量分析，从而建立在平面空间中对于线性变换的直觉理解，更进一步的理解$ \text{SVD} $和特征值/特征向量分别是如何描述一个线性变换的。具体的，这里观察了在该线性变换的作用下，一个点 $ (1,0) $ 是如何在两种矩阵变换下，映射到目标点的。

2. 奇异值分解

2.1 矩阵A的两种 SVD 分解

奇异值分解并不是唯一的。从几何的角度理解，一个二维空间的线性变换，是由旋转、反射、缩放组成，而先旋转、或先反射都是可以的，而这对应的就是不同的奇异值分解。考虑上述的矩阵 $ A = \begin{bmatrix} 1 & 2 \\ 2 & 1 \end{bmatrix} $ 进行 $ \text{SVD} $，我们有如下两种分解（关于具体的分解方法，本文并不详述）。

第一种分解：

$$ A = \begin{bmatrix}
1 & 2 \\
2 & 1
\end{bmatrix} = UΣV^T =\begin{bmatrix}
\frac{1}{\sqrt{2}} & -\frac{1}{\sqrt{2}} \\
\frac{1}{\sqrt{2}} & \frac{1}{\sqrt{2}}
\end{bmatrix}\begin{bmatrix}
3 & 0 \\
0 & 1
\end{bmatrix}\begin{bmatrix}
\frac{1}{\sqrt{2}} & \frac{1}{\sqrt{2}} \\
\frac{1}{\sqrt{2}} & -\frac{1}{\sqrt{2}}
\end{bmatrix}
$$

第二种分解如下：

$$ A = \begin{bmatrix}
1 & 2 \\
2 & 1
\end{bmatrix} = UΣV^T =\begin{bmatrix}
-\frac{1}{\sqrt{2}} & -\frac{1}{\sqrt{2}} \\
-\frac{1}{\sqrt{2}} & \frac{1}{\sqrt{2}}
\end{bmatrix}\begin{bmatrix}
3 & 0 \\
0 & 1
\end{bmatrix}\begin{bmatrix}
-\frac{1}{\sqrt{2}} & -\frac{1}{\sqrt{2}} \\
\frac{1}{\sqrt{2}} & -\frac{1}{\sqrt{2}}
\end{bmatrix} $$

2.2 分解1的几何意义与图示

$$ A = \begin{bmatrix}
1 & 2 \\
2 & 1
\end{bmatrix} = U\Sigma V^T = \begin{bmatrix}
\frac{1}{\sqrt{2}} & -\frac{1}{\sqrt{2}} \\
\frac{1}{\sqrt{2}} & \frac{1}{\sqrt{2}}
\end{bmatrix}\begin{bmatrix}
3 & 0 \\
0 & 1
\end{bmatrix}\begin{bmatrix}
\frac{1}{\sqrt{2}} & \frac{1}{\sqrt{2}} \\
\frac{1}{\sqrt{2}} & -\frac{1}{\sqrt{2}}
\end{bmatrix}
$$

考虑：

$ V^T = \begin{bmatrix} \frac{1}{\sqrt{2}} & \frac{1}{\sqrt{2}} \\ \frac{1}{\sqrt{2}} & -\frac{1}{\sqrt{2}}\end{bmatrix} $ 形式与 $ \begin{bmatrix} \cos \varphi & \sin\varphi \\ \sin\varphi & -\cos \varphi \end{bmatrix} $ 相同，故，此为关于直线 $ y = (\tan\frac{\varphi}{2})x $ 的反射^[附录1]。

$ \Sigma = \begin{bmatrix} 3 & 0 \\ 0 & 1 \end{bmatrix} $ 表示将点、向量的坐标进行缩放。

$ U = \begin{bmatrix} \frac{1}{\sqrt{2}} & -\frac{1}{\sqrt{2}} \\ \frac{1}{\sqrt{2}} & \frac{1}{\sqrt{2}} \end{bmatrix} $ 形式与 $ \begin{bmatrix} \cos \varphi & -\sin\varphi \\ \sin\varphi & \cos \varphi \end{bmatrix} $ 相同，故，此为一个逆时针 $ \varphi $ 度的旋转^[附录1]。

即，上述的线性变换可以做这样的理解：

先将点以$ y=\tan\frac{45}{2}x = (\sqrt{2}-1)x $为轴进行反射
然后将坐标第一个分量放大3倍
最后再逆时针旋转$ 45^{\circ} $

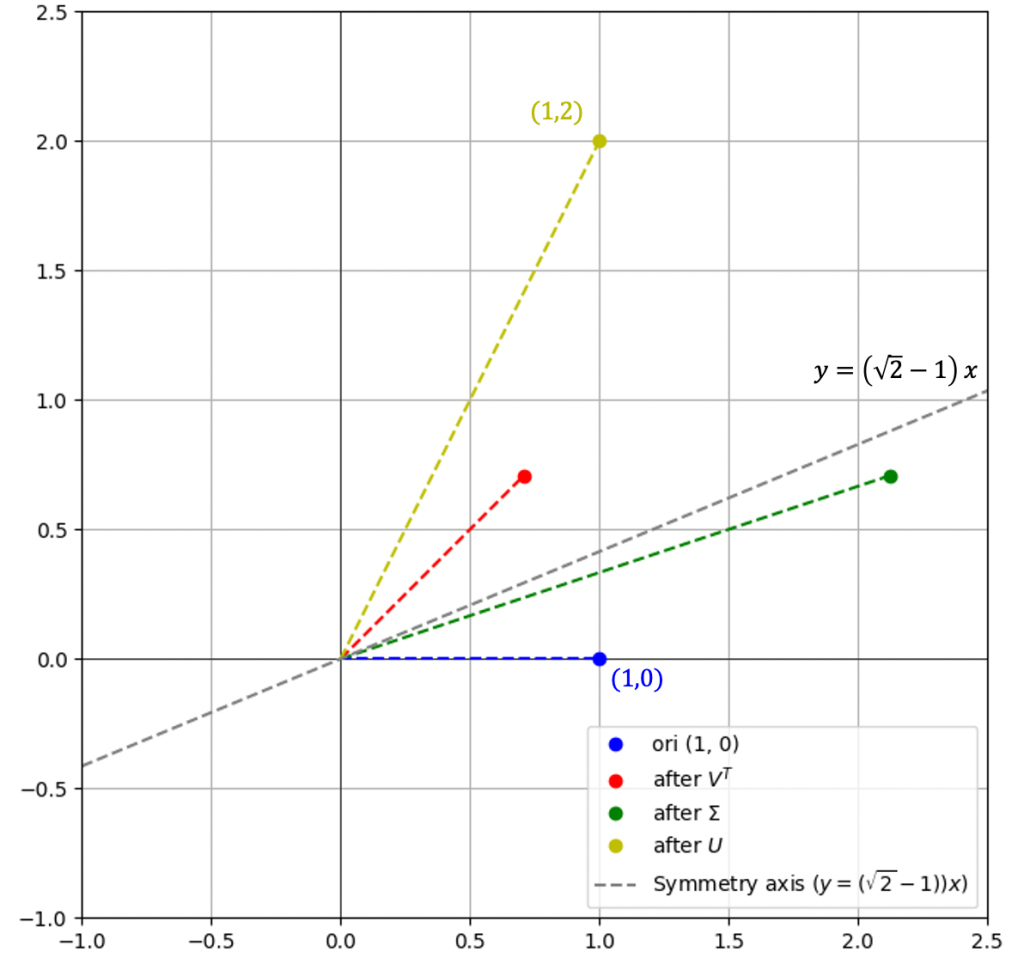
考虑坐标上的点$ \alpha = \begin{pmatrix} 1 \\ 0 \end{pmatrix} $，我们看看如何经过该线性变换，映射到目标点：

右图反映了完整的过程：

$ (1,0) $ 先经过按图中虚线为轴进行反射，到红点
然后，进行拉伸，第一个分量拉伸3倍，到绿色点
最后，再逆时针旋转$ 45^{\circ} $ 到黄色点

对应的矩阵计算如下：

$ \text{red} = V^T \alpha = \begin{bmatrix} \frac{1}{\sqrt{2}} & \frac{1}{\sqrt{2}} \\ \frac{1}{\sqrt{2}} & -\frac{1}{\sqrt{2}}\end{bmatrix} \begin{pmatrix} 1 \\ 0 \end{pmatrix} = \begin{pmatrix} \frac{1}{\sqrt{2}} \\ \frac{1}{\sqrt{2}} \end{pmatrix} $

$ \text{green} = \Sigma V^T \alpha = \Sigma \, \text{red} = \begin{bmatrix} 3 & 0 \\ 0 & 1 \end{bmatrix} \begin{pmatrix} \frac{1}{\sqrt{2}} \\ \frac{1}{\sqrt{2}} \end{pmatrix} = \begin{pmatrix} \frac{3}{\sqrt{2}} \\ \frac{1}{\sqrt{2}} \end{pmatrix} $

$ \text{yellow} = U\Sigma V^T \alpha = U \, \text{green} = \begin{bmatrix} \frac{1}{\sqrt{2}} & -\frac{1}{\sqrt{2}} \\ \frac{1}{\sqrt{2}} & \frac{1}{\sqrt{2}} \end{bmatrix} \begin{pmatrix} \frac{3}{\sqrt{2}} \\ \frac{1}{\sqrt{2}} \end{pmatrix} = \begin{pmatrix} 1 \\ 2 \end{pmatrix} $

2.3 分解2的几何意义与图示

考虑：

$ V^T = \begin{bmatrix}-\frac{1}{\sqrt{2}} & -\frac{1}{\sqrt{2}} \\ \frac{1}{\sqrt{2}} & -\frac{1}{\sqrt{2}} \end{bmatrix} $ 形式与 $ \begin{bmatrix} \cos \varphi & -\sin\varphi \\ \sin\varphi & \cos \varphi \end{bmatrix} $相同，故，此为一个逆时针 $ \varphi = 135^{\circ} $ 度的旋转^[附录1]。

$ \Sigma = \begin{bmatrix} 3 & 0 \\ 0 & 1 \end{bmatrix} $ 表示将点、向量的坐标进行缩放。

$ U = \begin{bmatrix} -\frac{1}{\sqrt{2}} & -\frac{1}{\sqrt{2}} \\ -\frac{1}{\sqrt{2}} & \frac{1}{\sqrt{2}} \end{bmatrix} $ 形式与 $ \begin{bmatrix} \cos \varphi & \sin\varphi \\ \sin\varphi & -\cos \varphi \end{bmatrix} $ 相同，故，此为关于直线 $ y = (\tan\frac{\varphi}{2})x $ 的反射^[附录1]。

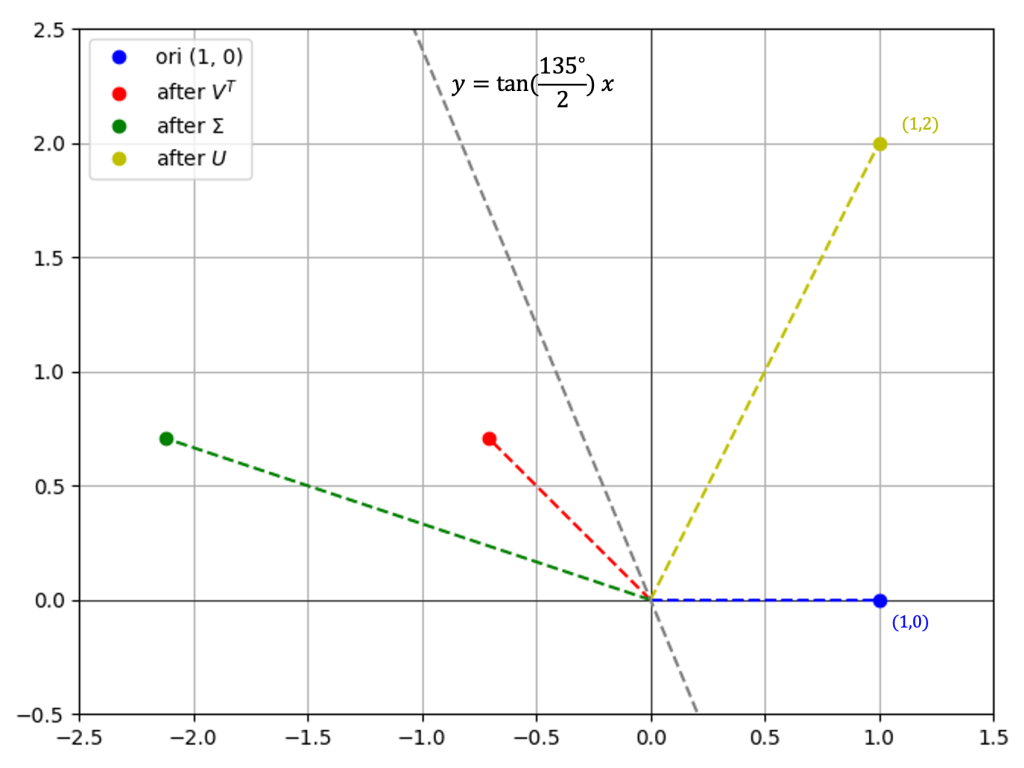
即，上述的线性变换可以做这样的理解：

点$ (1,0) $ 先逆时针旋转$ \varphi = 135^{\circ} $到达红色点
然后将坐标第一个分量放大3倍，成为绿色点
最后将点以$ y=\tan\frac{-135^{\circ}}{2}x $为轴进行反射，到黄色点

具体可以参考右图，详细的计算这里不再给出。

3. 特征值与特征向量

因为这里的$ A $是一个 $ 2 \times 2 $ 的方阵，故可以使用特征值与特征向量来洞察这个线性变换的本质。

对于该矩阵的特征值、对应的特征向量计算结果如下：

对于特征值 $ \lambda_1 = 3 $ 时，特征向量为 $ (\frac{1}{\sqrt{2}}, \frac{1}{\sqrt{2}}) $
对于特征值 $ \lambda_2 = -1 $ 时，特征向量为 $ (\frac{1}{\sqrt{2}}, -\frac{1}{\sqrt{2}}) $

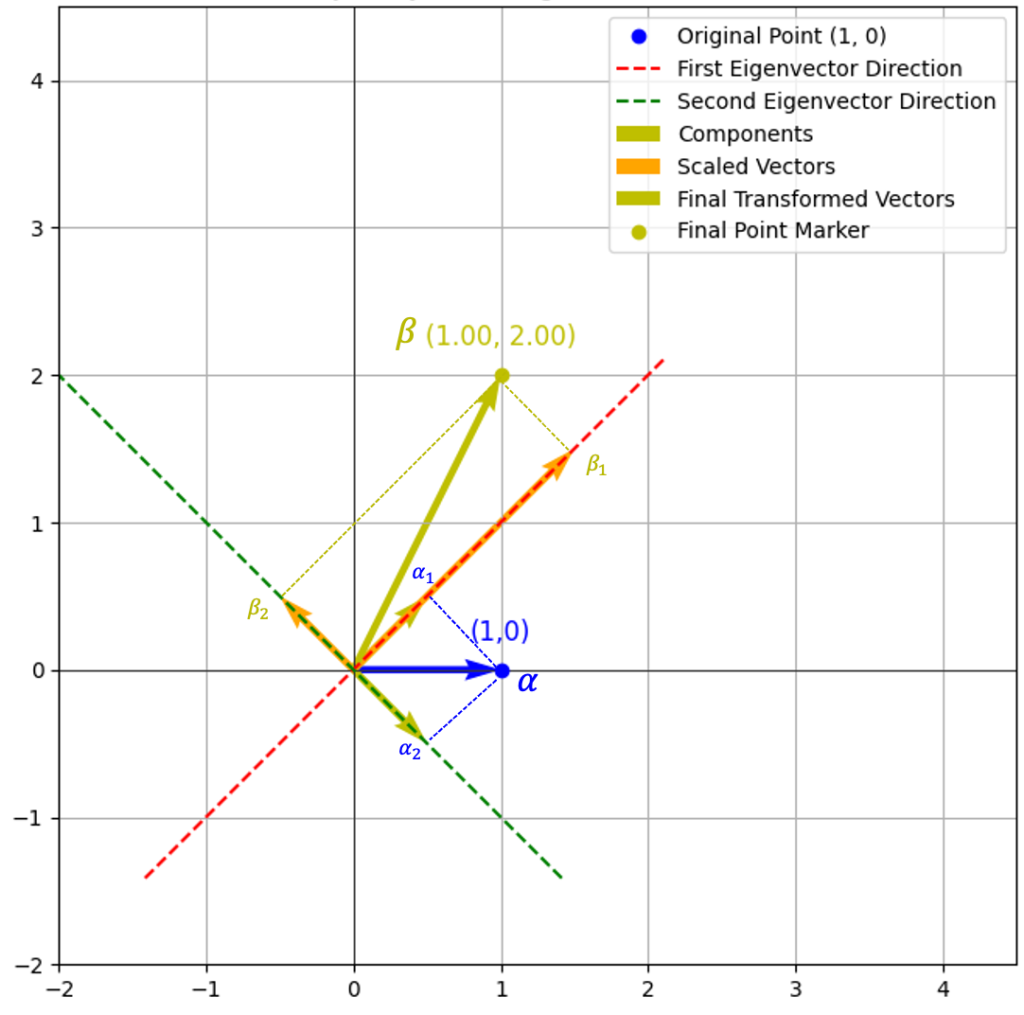
依旧，这里我们来考虑向量 $ \alpha = \begin{pmatrix} 1 \\ 0 \end{pmatrix} $ 在这两个特征向量方向上作用后的效果。

右图已经比较直观的反应了如何从特征向量和特征值的角度去理解线性变换：

首先，先将向量 $ \alpha $ 在两个特征向量上进行分解，分解后的向量分别为 $ \alpha_1 \, \alpha_2 $
然后再按照特征值进行缩放：
- $ \lambda_1 = 3 $ 故将 $ \alpha_1$拉伸为 $ \beta_1 $
- $ \lambda_2 = -1 $ 故将 $ \alpha_2$反向为 $ \beta_2 $
最后，$ \beta_1 $ 和 $ \beta_2 $ 合并为 $ \beta $

4. 小结

在这种情况下（注：线性变换矩阵为一个 $ 2 \times 2 $的满秩矩阵），我们可以使用奇异值分解$ \text{SVD} $、特征值计算的方式来洞察这个线性变换的“本质”。两种方法各有一些优缺点，大家可以自己去体会，这里小结一下我的理解。

奇异值分解$ \text{SVD} $是一种“动态”的展示线性变换的方法，可以让你很清晰的了解这个线性变换是如何将空间中的“一个点”映射到“另一个点”的。例如在上述的例子中，则是先进行旋转、然后进行缩放、最后进行反射。

特征值/特征向量计算则是对线性变换的“静态”解释，使用静态的方式展现了线性变换如何将“一个点”映射到“另一个点”的。

5. 补充说明

实际应用中的奇异值分解通常是用于处理更高维的向量空间，所以通常没有这么直观的几何意义，但是依旧可以使用类比的“反射”、“旋转”、“拉伸/压缩”等概念去扩展的理解。
特征值/特征向量仅适用于处理方阵的场景，所以场景比较受限。
关于特特征值/特征向量计算，在实际中可能会更加复杂，例如，重根、复数根等情况，要想进一步理解，则需要做更深入的研究。
要进一步加深理解，则可以考虑，观察一个三维空间中变换的实例，有一些相同，也有一些不同：
- 反射，通常是基于某个平面（两个基张成的平面）的
- 选择，则是绕着某个直线（某个向量的方向上）

附录1 二维空间的正交变换

二维空间中，有两种正交变换，即旋转或反射。其对应的线性变换矩阵分别有如下的形式：$ \begin{bmatrix} \cos \varphi & \sin\varphi \\ \sin\varphi & -\cos \varphi \end{bmatrix} $ 与 $ \begin{bmatrix} \cos \varphi & -\sin\varphi \\ \sin\varphi & \cos \varphi \end{bmatrix} $ 。

附录2 三维空间的正交变换

在三维空间内，对于一组规范正交基 $ \{ \alpha_1,\alpha_2,\alpha_3 \} $ ，该空间下的正交变换矩阵总有如下形式：

$$
\begin{bmatrix}
\pm 1 & 0 & 0 \\
0 & a & b \\
0 & c & c
\end{bmatrix}
$$

更为具体的为如下三种形态之一：

$$
A = \begin{bmatrix}
1 & 0 & 0 \\
0 & \cos\varphi & -\sin\varphi \\
0 & \sin\varphi & \cos\varphi
\end{bmatrix}
\quad
B = \begin{bmatrix}
-1 & 0 & 0 \\
0 & 1 & 0 \\
0 & 0 & 1
\end{bmatrix}
\\ \begin{align}
C & = \begin{bmatrix}
-1 & 0 & 0 \\
0 & \cos\varphi & -\sin\varphi \\
0 & \sin\varphi & \cos\varphi
\end{bmatrix} \\
& =
\begin{bmatrix}
1 & 0 & 0 \\
0 & \cos\varphi & -\sin\varphi \\
0 & \sin\varphi & \cos\varphi
\end{bmatrix}
\begin{bmatrix}
-1 & 0 & 0 \\
0 & 1 & 0 \\
0 & 0 & 1
\end{bmatrix}
\end{align}
$$

这里的：

变换 $ A $ 为一个旋转，旋转轴为 $ \alpha_1 $ 所在的直线
变换 $ B $ 是一个反射，反射轴平面为 $ \mathscr{L}(\alpha_2,\alpha_3) $
变换 $ C $ 是上述两个变换的组合

2 responses to “奇异值分解–深度学习的数学基础”

Hallo Mad

2025-09-22

Barbarslot kini menjadi salah satu bentuk hiburan digital yang digemari banyak orang. Selain mudah dimainkan, variasi tema dan fitur bonus menjadikannya menarik bagi pemain kasual hingga penggemar lama. Beberapa permainan slot dirancang dengan tingkat pengembalian (RTP) tinggi, memberikan peluang lebih besar untuk meraih hadiah.
Silent Is Golden

2025-09-24

Om88 menawarkan pengalaman bermain seru dengan peluang menang besar, permainan mudah, dan grafis menarik yang cocok untuk hiburan santai.

orczhou.com