目录
在整个大语言模型学习之路中,对 Attention 机制的理解大概是最为让我困惑的部分,最终经过层层解构、加上重新把“线性代数”温习了一遍之后,最终,总算某种程度的理解了 Attention 机制的设计。相信对于所有NLP专业的人,这部分都是不太容易理解的。
1. 概述
要想讲清楚,大概也是非常不容易的,这里就做一个尝试吧。这里的重点是讲清楚 Attention Score (简称Attention)的计算。介绍的顺序是“两个词语的相似度”、“Similarity Score Matrix”、“Attention Score Matrix”。
1.1 要构建的是直觉,而不是“推理”
为什么 Attention 理解起来很难呢?我想其中有一个原因大概是这个“机制”本身并不是某种“公式推导”出来的,而是通过一篇篇论文与实践,被证明非常有效的一个机制,所以,这个机制本身的所具备的“可解释性”其实也是有限的。这大概也是,无论你在互联网上如何搜索,也没有谁可以比较简单的把这个机制说清楚的原因。但,理解这个机制构建的直觉,对于理解整个 Transformer ,以及整个当代大语言模型技术基础都是至关重要的。
2. 预处理
在“大语言模型的输入:tokenize”中详细介绍了“提示词”进入大模型处理之前,如何将提示词换行成大模型可以处理的“词向量”或者说“token embedding”。
大语言模型在开始“Attention”计算之前,还会对“token embedding”进行一些预处理,这些预处理包括了“融入”位置向量、对向量进行“归一化”处理(将各个向量都转化为均值为0、方差为1的向量,长度要统一变成1吗?)。
例如,在这里的例子中,提示词 “It’s very hot in summer. Swimming is”,先转换为embedding,然后加上位置编码(positional encoder)、再进行正规化,最后变换为如下的向量 “ X ” :
|-------------------------------------------------------------------------------------------------------------------------------------------
| Token | wte[:3] (word token embedding) | wpe[:3](word positional e..)| wte [:3] + wpe [:3] | X[:3] (Norm) |
|-------------------------------------------------------------------------------------------------------------------------------------------
|It | [0.039, -0.0869, 0.0662 ,...] | [-0.0188, -0.1974, 0.004 ] | [0.0202, -0.2844,0.0702 ] | [ 0.0129, -0.1104, -0.0317,...] |
|âĢ | [-0.075, 0.0948, -0.0034,...] | [0.024, -0.0538, -0.0949] | [-0.051, 0.041, -0.0982] | [-0.0530, 0.0588, -0.1290,...] |
|Ļ | [-0.0223, 0.0182, 0.2631 ,...] | [0.0042, -0.0848, 0.0545 ] | [-0.0181,-0.0666,0.3176 ] | [-0.0170, -0.0242, 0.1639,...] |
|s | [-0.064, -0.0469, 0.2061 ,...] | [-0.0003, -0.0738, 0.1055 ] | [-0.0643,-0.1207,0.3116 ] | [-0.0754, -0.0842, 0.1842,...] |
|Ġvery | [-0.0553, -0.0348, 0.0606 ,...] | [0.0076, -0.0251, 0.127 ] | [-0.0477,-0.0599,0.1876 ] | [-0.0566, -0.0280, 0.0953,...] |
|Ġhot | [0.0399, -0.0053, 0.0742 ,...] | [0.0096, -0.0339, 0.1312 ] | [0.0495, -0.0392,0.2054 ] | [ 0.0587, -0.0086, 0.1073,...] |
|Ġin | [-0.0337, 0.0108, 0.0293 ,...] | [0.0027, -0.0205, 0.1196 ] | [-0.031, -0.0098,0.149 ] | [-0.0391, 0.0209, 0.0731,...] |
|Ġsummer | [0.0422, 0.0138, -0.0213,...] | [0.0025, -0.0032, 0.1174 ] | [0.0448, 0.0106, 0.0961 ] | [ 0.0532, 0.0397, 0.0181,...] |
|. | [0.0466, -0.0113, 0.0283 ,...] | [-0.0012, -0.0018, 0.111 ] | [0.0454, -0.0131,0.1394 ] | [ 0.0553, 0.0152, 0.0579,...] |
|ĠSw | [0.0617, 0.0373, 0.1018 ,...] | [0.0049, 0.0021, 0.1178 ] | [0.0666, 0.0395, 0.2196 ] | [ 0.0807, 0.0691, 0.1216,...] |
|imming | [-0.1385, -0.1774, -0.0181,...] | [0.0016, 0.0062, 0.1004 ] | [-0.1369,-0.1711,0.0823 ] | [-0.1528, -0.1249, -0.0017,...] |
|Ġis | [-0.0097, 0.0101, 0.0556 ,...] | [-0.0036, 0.0175, 0.1068 ] | [-0.0133,0.0275, 0.1623 ] | [-0.0175, 0.0605, 0.0880,...] |
|-------------------------------------------------------------------------------------------------------------------------------------------
这里的 “X” 是一个由12个 “token embedding”组成的矩阵,“形状”是 12 x 768 。在数学符号上,有:
--------------------------------------- ------------------------------------------ -------------
| [ 0.0129, -0.1104, -0.0317,...] | | x_1 = [ 0.0129, -0.1104, -0.0317,...] | |It |
| [-0.0530, 0.0588, -0.1290,...] | | x_2 = [-0.0530, 0.0588, -0.1290,...] | |âĢ |
| [-0.0170, -0.0242, 0.1639,...] | | x_3 = [-0.0170, -0.0242, 0.1639,...] | |Ļ |
| [-0.0754, -0.0842, 0.1842,...] | | x_4 = [-0.0754, -0.0842, 0.1842,...] | |s |
| [-0.0566, -0.0280, 0.0953,...] | | x_5 = [-0.0566, -0.0280, 0.0953,...] | |Ġvery |
| X = [ 0.0587, -0.0086, 0.1073,...] | | x_6 = [ 0.0587, -0.0086, 0.1073,...] | |Ġhot |
| [-0.0391, 0.0209, 0.0731,...] | | x_7 = [-0.0391, 0.0209, 0.0731,...] | |Ġin |
| [ 0.0532, 0.0397, 0.0181,...] | | x_8 = [ 0.0532, 0.0397, 0.0181,...] | |Ġsummer |
| [ 0.0553, 0.0152, 0.0579,...] | | x_9 = [ 0.0553, 0.0152, 0.0579,...] | |. |
| [ 0.0807, 0.0691, 0.1216,...] | | x_10 = [ 0.0807, 0.0691, 0.1216,...] | |ĠSw |
| [-0.1528, -0.1249, -0.0017,...] | | x_11 = [-0.1528, -0.1249, -0.0017,...] | |imming |
| [-0.0175, 0.0605, 0.0880,...] | | x_12 = [-0.0175, 0.0605, 0.0880,...] | |Ġis |
--------------------------------------- ------------------------------------------ -------------
3. Similarity Score Matrix
在正式介绍 Attention 之前,为了能够比较好的理解“为什么”是这样,这里先引入了“Similarity”的概念,最终在该概念上,新增权重矩阵,就是最终的 Attention :
$$ \text{Similarity} = \text{softmax}(\frac{XX^{T}}{\sqrt{d}})X $$
这里删除了参数矩阵:\(W^Q \quad W^K \quad W^V \)
$$ \text{Attention} = \text{softmax}(\frac{QK^{T}}{\sqrt{d}})V $$
其中, \(Q = XW^Q \quad K = XW^K \quad V = XW^V \)
3.1 两个“词语”的相似度
在向量为单位长度的时候,通常可以直接使用“内积”作为两个向量的相似度度量。例如,考虑词语 “hot” 与 “summer” 的相似度,则可以“简化”的处理这两个词(Token)的向量的“内积”。
在前面的文章“大语言模型的输入:tokenize”中,较为详细的介绍了大语言模型如何把一个句子转换成一个的 Token,然后再转换为一个个“向量”。那么,我们通常会通过两个向量的余弦相似度来描述其相似度,如果向量的“长度”(\(L_2 \) 范数)是单位长度,那么也通常会直接使用“内积”描述两个向量的相似度:
$$
\cos \theta = \frac{\alpha \cdot \beta}{\|\alpha\| \|\beta\| }
$$
\(f(x) = \cos(x) \) 的图像如右图,故:
- 夹角为 0 时,最为相似,这时候 \(\cos(x) = 1 \)
- 夹角 \(\pi \) 时,最“不”相似,这时候 \(\cos(x) = 0 \)
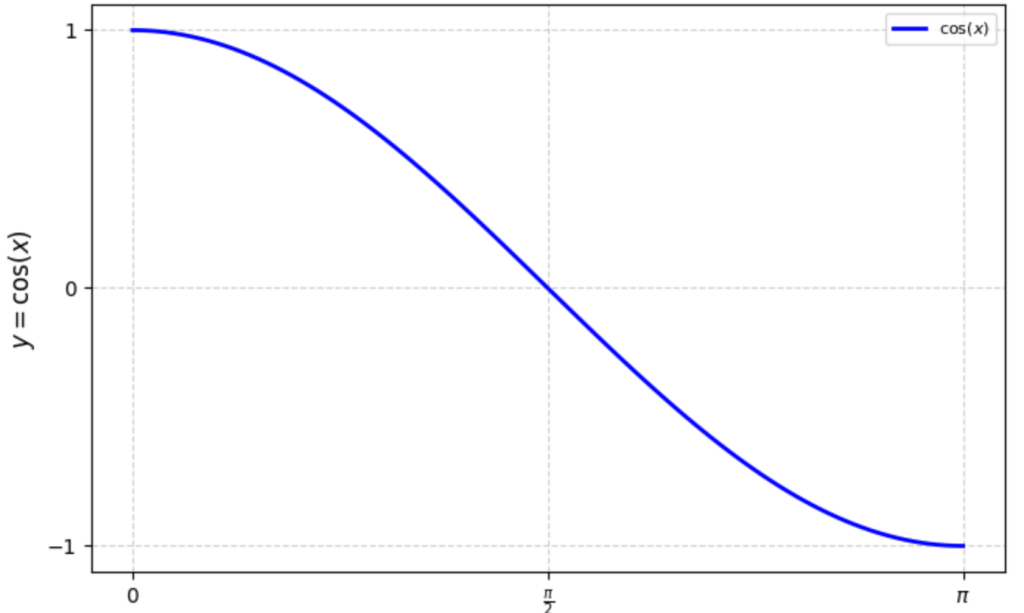
例如,
3.2 “Similarity Score Matrix”
因为两个向量的“内积”某种程度可以表示为相似度。那么,对于句子中的某个 token 来说,与其他所有向量各自计算“内积”,就可以获得一个与其他所有向量“相似程度”的数组,再对这个数组进行 softmax 计算就可以获得一个该 token 与其他所有向量“相似程度”的归一化数组。这个归一化的数据,就可以理解为这里的“Similarity Score Matrix”。
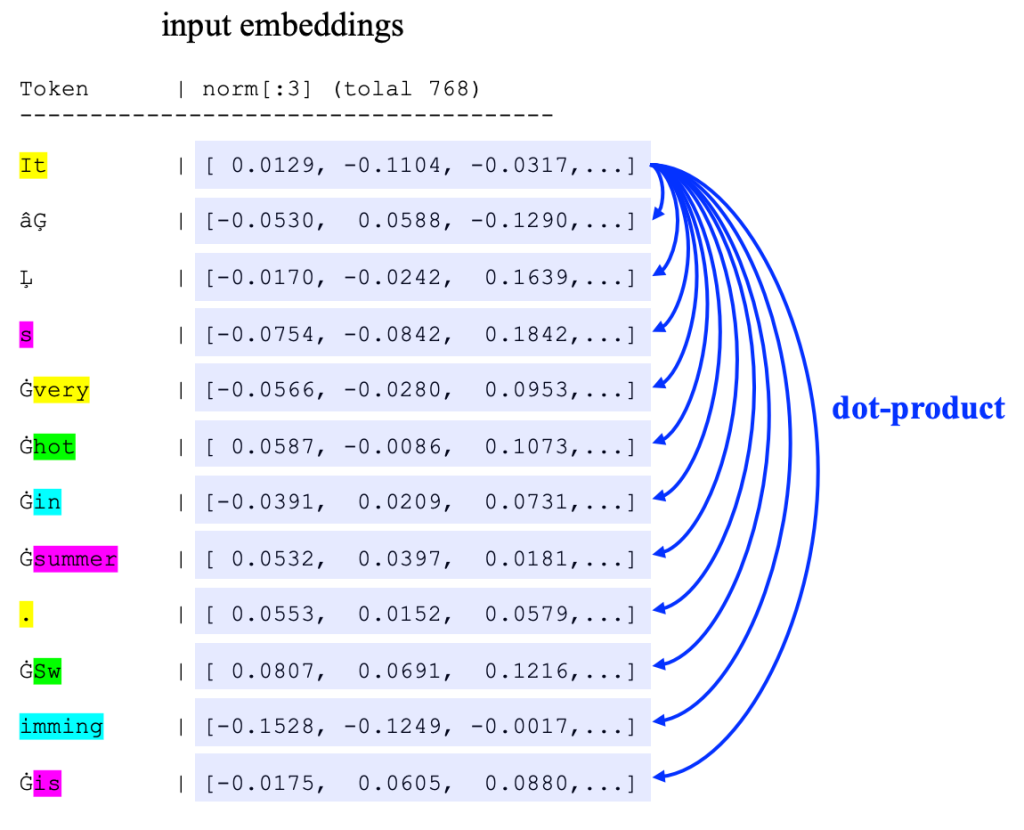
这里依旧以“大语言模型的输入:tokenize”示例中的句子为演示示例。
更为具体的,可以参考右图。这里考虑 Token “It” 与其他所有词语的相似度。即计算 Token “It” 的 Embedding 向量,与其他所有向量的“内积”。
更进一步,如果计算两两词语之间的相似度,并进行归一化(softmax ),则有如下的Similarity Matrix:
[0.6975, 0.0347, 0.0236, 0.0298, 0.0386, 0.0282, 0.0272, 0.0270, 0.0216, 0.0244, 0.0219, 0.0254]
[0.0000, 0.9994, 0.0002, 0.0000, 0.0000, 0.0001, 0.0000, 0.0000, 0.0000, 0.0001, 0.0001, 0.0000]
[0.0000, 0.0004, 0.9987, 0.0001, 0.0001, 0.0001, 0.0000, 0.0002, 0.0000, 0.0001, 0.0002, 0.0000]
[0.0002, 0.0003, 0.0004, 0.9945, 0.0008, 0.0004, 0.0011, 0.0003, 0.0007, 0.0005, 0.0002, 0.0007]
[0.0013, 0.0012, 0.0013, 0.0042, 0.9724, 0.0044, 0.0047, 0.0021, 0.0030, 0.0013, 0.0012, 0.0028]
[0.0002, 0.0003, 0.0003, 0.0004, 0.0009, 0.9932, 0.0005, 0.0020, 0.0004, 0.0009, 0.0006, 0.0003]
[0.0049, 0.0048, 0.0038, 0.0299, 0.0258, 0.0125, 0.7728, 0.0086, 0.0779, 0.0095, 0.0025, 0.0471]
[0.0001, 0.0001, 0.0005, 0.0002, 0.0003, 0.0015, 0.0002, 0.9959, 0.0002, 0.0003, 0.0003, 0.0002]
[0.0049, 0.0048, 0.0045, 0.0255, 0.0203, 0.0126, 0.0974, 0.0082, 0.7698, 0.0094, 0.0024, 0.0401]
[0.0001, 0.0001, 0.0001, 0.0002, 0.0001, 0.0003, 0.0001, 0.0002, 0.0001, 0.9983, 0.0002, 0.0002]
[0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.9998, 0.0000]
[0.0033, 0.0027, 0.0028, 0.0129, 0.0110, 0.0063, 0.0334, 0.0055, 0.0228, 0.0075, 0.0025, 0.8893]
在这个示例中,则会有上述 12×12 的矩阵。该矩阵反应了“词”与“词”之间的相似度。如果,我们把每一行再进行一个“归一化”(注右图已经经过了归一化),那么每一行,就反应了一个词语与其他所有词语相似程度的一个度量。
例如,右图中 it 可能与 very 最为相似(除了自身)。
4. Self-Attention
4.1 对比
注意到最终的 “Attention” 计算公式和上述的“Similarity Score Matrix”的差别就是参数矩阵W:
$$ \text{Similarity Score} = \text{softmax}(\frac{XX^{T}}{\sqrt{d}})X $$
这里没有参数矩阵:\(W^Q \quad W^K \quad W^V \)
$$ \text{Attention} = \text{softmax}(\frac{QK^{T}}{\sqrt{d}})V $$
其中, \(Q = XW^Q \quad K = XW^K \quad V = XW^V \)
4.2 为什么需要参数矩阵 W
那么,为什么需要 \(W^Q \,, W^K \,, W^V \) 呢?这三个参数矩阵乘法,意味着什么呢?要说清楚、要理解这个点并不容易,也没有什么简单的描述可以说清楚的,这也大概是为什么,对于非 NLP 专业的人,要想真正理解 Transformer 或 Attention 是比较困难的。
你可能会看到过一种比较普遍的、简化版本,大概是说 \(W^Q \) 是一个 Query 矩阵,表示要查询什么;\(W^K \) 是一个 Key 矩阵,表示一个词有什么。这个说法似乎并不能增加对上述公式的理解。
那么,一个向量乘以一个矩阵时,这个“矩阵”意味着什么?是的,就是“线性变换”。
4.3 线性变换 Linear Transformations
一般来说,\(W^Q \,, W^K \,, W^V \) 是一个 \(d \times d \) 的矩阵[1]。对于的 Token Embedding (上述的矩阵 X )所在的向量空间,那么 \(W^Q \,, W^K \,, W^V \) 就是该向量空间的三个“线性变换”。
那么线性变换对于向量空间的作用是什么呢?这里我们以“奇异值分解”的角度来理解这个问题[2],即对向量进行拉伸/压缩、旋转、镜像变换。\(W^Q \,, W^K \,, W^V \) 则会分别对向量空间的向量(即Token Embedding)做类似的变换。变换的结果即为:
$$ Q = XW^Q \quad \quad K = XW^K \quad \quad V = XW^V $$
那么,如果参数矩阵“设计”合理,“Token”与“Token”之间就可以建立“期望”的 Attention 关系,例如:“代词”(it),总是更多的关注于“名词”;“名词”更多的关注与附近的“形容词”;再比如,“动词”更多关注前后的“名词”等。除了词性,线性变换关注的“维度”可能有很多,例如“位置”、“情感”、“动物”、“植物”、“积极/消极”等。关于如何理解 token embedding 的各个“维度”含义可以参考:Word Embedding 的可解释性探索。
当然,这三个参数矩阵都不是“设计”出来的,而是“训练”出来的。所以,要想寻找上述如此清晰的“可解释性”并不容易。2019年的论文《What Does BERT Look At? An Analysis of BERT’s Attention》较为系统的讨论了这个问题,感兴趣的可以去看看。
关于线性变换如何作用在向量空间上,可以参考:线性代数、奇异值分解–深度学习的数学基础。
所以,\( \frac{QK^T}{\sqrt{d}} = \frac{XW^Q (XW^K)^T}{\sqrt{d}} \) 则可以系统的表示,每个“Token”对于其他“Token”的关注程度(即pay attention的程度)。可以注意到:
- 增加了参数矩阵\(W^Q \,, W^K \,, W^V \)后,前面的“相似性”矩阵,就变为“注意力”矩阵
- “Token” 之间的关注程度不是对称的。例如 Token A 可能很关注 B;但是 B 可能并不关注 A
- 这里的 \(\sqrt{d} \) 根据论文描述,可以提升计算性能;
如果,你恰好理解了上面所有的描述,大概会有点失望的。就只能到这儿吗?似乎就只能到这里了。如果,你有更深刻的理解,欢迎留言讨论。
接下里,我们来看看 “Attention Score Matrix” 的计算。
4.4 Attention Score Matrix
使用上述的 “Similarity Score Matrix” 的计算方式,可以计算类似的 “Attention Score Matrix”,之后再对该矩阵进行 softmax 计算就可以获得每个词语对于其他所有词语的 Attention Score,或者叫“关注程度”。有了这个关注程度,再乘以 V 矩阵,原来的 Token Embedding 就变换为一个新的带有上下文的含义的 Token Eembedding 了,即 Context Embedding[3]。
类似的,我们有右图的 Attention Score Matrix 计算。
该矩阵反应了两个 Token 之间的 Attention 关系。该关系,通过对经过线性变换的 Token Embedding ,再进行内积计算获得。
Attention Score Matrix (12 x 12)
It âĢ Ļ s Ġvery Ġhot Ġin Ġsummer . ĠSw imming Ġis
-----------------------------------------------------------------------------------
It [ 0.14, -1.53, -1.45, -1.71, -1.69, -1.74, -2.36, -2.27, -2.37, -1.33, -0.58, -2.40] |
âĢ [ 0.70, -0.93, -1.72, -1.02, -1.52, -2.24, -1.90, -2.19, -1.63, -2.13, -1.66, -2.14] |
Ļ [-0.60, -1.81, -1.99, -1.96, -2.57, -1.84, -1.62, -2.04, -0.98, -1.18, -2.23, -2.25] |
s [-0.46, -1.33, -1.60, -2.65, -2.24, -1.99, -2.89, -1.44, -2.05, -2.77, -2.09, -2.74] |
Ġvery [ 0.29, -1.42, -1.77, -1.15, -0.94, -1.14, -1.81, -1.04, -1.77, -2.13, -0.60, -0.82] |
Ġhot [ 0.03, -0.68, -0.59, -0.95, -1.78, -0.10, -0.95, -0.14, -1.32, -0.57, 0.06, -1.07] 12
Ġin [-0.71, -1.72, -1.53, -2.18, -1.67, -1.93, -3.41, -1.69, -2.74, -1.89, -1.17, -2.02] rows
Ġsummer [-0.34, -1.49, -1.35, -1.31, -1.12, -0.89, -1.49, -1.11, -1.51, -1.15, -1.45, -1.20] |
. [-0.89, -1.73, -2.67, -2.80, -2.45, -2.37, -4.39, -2.33, -4.42, -2.73, -1.82, -3.21] |
ĠSw [-0.05, -1.15, -1.76, -1.15, -1.68, -0.74, -1.15, -1.35, -1.36, -1.29, -0.43, -1.51] |
imming [-0.02, -1.65, -0.87, -0.35, -1.18, -0.65, -0.33, -1.25, -0.38, -1.68, -2.15, -1.08] |
Ġis [-0.97, -2.03, -2.56, -2.94, -1.96, -2.71, -4.07, -2.46, -3.51, -2.68, -1.88, -2.99] |
-----------------------------------------------------------------------------------
|<----------------------------- columns: 12 -------------------------------------->|
4.5 Masked Attention Score Matrix
上述计算,是一个典型的 Self Attention 计算过程,BERT 模型就使用类似的计算,但 GPT 模型(或者叫 Decoder 模型)还有一些不同。GPT 模型中为了训练出更好的从现有 Token 中生成新 Token 的模型,将上述的 Self Attention 更改成了 Masked Self Attention ,即将 Attention Score Matrix 的右上角部分全部置为 -inf (即负无穷),后续经过 softmax 之后这些值都会变成零,即,在该类模型下,一个词语对于其后面的词的关注度为 0 。
在 Decoder 模型设计中,为了生成更准确的下一个 Token 所以在训练和推理中,仅会计算Token 对之前的 Token 的 Attention ,所以上述的矩阵的右上角部分就会被遮盖,即就是右侧的 “Masked Attention Score Matrix”。
Masked Attention Score Matrix (12 x 12)
It âĢ Ļ s Ġvery Ġhot Ġin Ġsummer . ĠSw imming Ġis
---------------------------------------------------------------------------------------
It [ 0.14, -inf, -inf, -inf, -inf, -inf, -inf, -inf, -inf, -inf, -inf, -inf] |
âĢ [ 0.70, -0.93, -inf, -inf, -inf, -inf, -inf, -inf, -inf, -inf, -inf, -inf] |
Ļ [-0.60, -1.81, -1.99, -inf, -inf, -inf, -inf, -inf, -inf, -inf, -inf, -inf] |
s [-0.46, -1.33, -1.60, -2.65, -inf, -inf, -inf, -inf, -inf, -inf, -inf, -inf] |
Ġvery [ 0.29, -1.42, -1.77, -1.15, -0.94, -inf, -inf, -inf, -inf, -inf, -inf, -inf] |
Ġhot [ 0.03, -0.68, -0.59, -0.95, -1.78, -0.10, -inf, -inf, -inf, -inf, -inf, -inf] 12
Ġin [-0.71, -1.72, -1.53, -2.18, -1.67, -1.93, -3.41, -inf, -inf, -inf, -inf, -inf] rows
Ġsummer [-0.34, -1.49, -1.35, -1.31, -1.12, -0.89, -1.49, -1.11, -inf, -inf, -inf, -inf] |
. [-0.89, -1.73, -2.67, -2.80, -2.45, -2.37, -4.39, -2.33, -4.42, -inf, -inf, -inf] |
ĠSw [-0.05, -1.15, -1.76, -1.15, -1.68, -0.74, -1.15, -1.35, -1.36, -1.29, -inf, -inf] |
imming [-0.02, -1.65, -0.87, -0.35, -1.18, -0.65, -0.33, -1.25, -0.38, -1.68, -2.15, -inf] |
Ġis [-0.97, -2.03, -2.56, -2.94, -1.96, -2.71, -4.07, -2.46, -3.51, -2.68, -1.88, -2.99] |
---------------------------------------------------------------------------------------
|<----------------------------- columns: 12 -------------------------------------->|
通常为了快速计算对于上述的计算值会除以 \(\sqrt{d} \) ,可以提升计算的效率。
4.6 归一化(softmax) Attention Score
对于上述矩阵的每一行都进行一个 softmax 计算,就可以获得一个归一化的按照百分比分配的Attention Score。
经过归一化之后,每个词语对于其他词语的 Attention 程度都可以使用百分比表达处理。例如,“summer”对于“It”的关注程度最高,为26%;其次是关注“hot”,为15%。可以看到这一组线性变换(\(W^Q\,W^K \))对于第一个位置表达特别的关注。
The Attention Score Matrix (12 x 12)
It âĢ Ļ s Ġvery Ġhot Ġin Ġsummer . ĠSw imming Ġis
-----------------------------------------------------------------------------
It [1.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00] |
âĢ [0.84 0.16 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00] |
Ļ [0.65 0.19 0.16 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00] |
s [0.54 0.23 0.17 0.06 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00] |
Ġvery [0.54 0.10 0.07 0.13 0.16 0.00 0.00 0.00 0.00 0.00 0.00 0.00] |
Ġhot [0.29 0.14 0.16 0.11 0.05 0.25 0.00 0.00 0.00 0.00 0.00 0.00] 12
Ġin [0.36 0.13 0.16 0.08 0.14 0.11 0.02 0.00 0.00 0.00 0.00 0.00] rows
Ġsummer [0.26 0.08 0.09 0.10 0.12 0.15 0.08 0.12 0.00 0.00 0.00 0.00] |
. [0.40 0.17 0.07 0.06 0.08 0.09 0.01 0.10 0.01 0.00 0.00 0.00] |
ĠSw [0.27 0.09 0.05 0.09 0.05 0.14 0.09 0.07 0.07 0.08 0.00 0.00] |
imming [0.19 0.04 0.08 0.14 0.06 0.10 0.14 0.06 0.13 0.04 0.02 0.00] |
Ġis [0.30 0.10 0.06 0.04 0.11 0.05 0.01 0.07 0.02 0.05 0.12 0.04] |
-----------------------------------------------------------------------------
|<----------------------------- columns: 12 --------------------------->|
4.7 Contextual Embeddings
最后,再按照上述的 Attention Matrix 的比例,将各个 Token Embedding 进行一个“加权平均计算”。
例如,上述的加权计算时,“summer” 则会融入 26% 的“It”,15%的“hot”… ,最后生成新的 “summer” 的表达,这个表达也可以某种程度理解为 “Contextual Embeddings”。需要注意的是,这里在计算加权平均,也不是直接使用原始的 Token Embedding ,也是一个经过了线性变换的Embedding,该线性变换矩阵也是经过训练而来的,即矩阵 \(W^V \)。
例如,上述的加权计算时,“summer” 则会融入 26% 的“It”,15%的“hot”… ,最后生成新的 “summer” 的表达,这个表达也可以某种程度理解为 “Contextual Embeddings”。
需要注意的是,这里在计算加权平均,也不是直接使用原始的 Token Embedding ,也是一个经过了线性变换的Embedding,该线性变换矩阵也是经过训练而来的,即矩阵 \(W^V \)。
Token | Contextual Embeddings(12 x 768)
--------------------------------------------
It | [ 0.0452, 0.0628, 0.1463,...]
âĢ | [ 0.0153, 0.0752, 0.1247,...]
Ļ | [ 0.0034, 0.0464, 0.0923,...]
s | [-0.0082, 0.0464, 0.0801,...]
Ġvery | [ 0.0218, 0.1029, 0.0621,...]
Ġhot | [ 0.0327, 0.0892, 0.0409,...]
Ġin | [ 0.0249, 0.0964, 0.0329,...]
Ġsummer | [ 0.0583, 0.1195, 0.0068,...]
. | [ 0.0334, 0.1100, 0.0366,...]
ĠSw | [ 0.0086, 0.0846, 0.0074,...]
imming | [-0.0049, 0.0841, -0.0339,...]
Ġis | [ 0.0410, 0.0706, 0.0077,...]
5 计算示意图
如下的示意图,一定的可视化的表达了,一个 Token 如何经过上述的矩阵运算,如何了其他 Token 的内容。
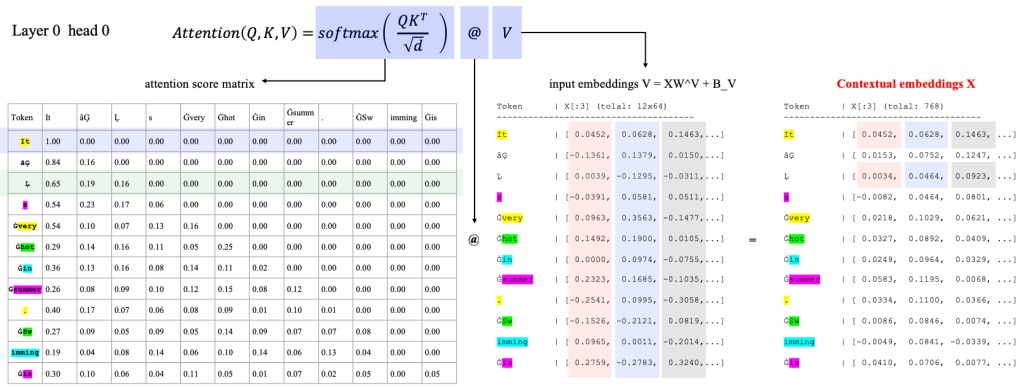
6. 注意力矩阵的观察
那么,我们给定于如下的提示词输入:“Martin’s one of my sons, and the other is Chanler.”。看看在 GPT 模型中,各个Token之间的 Attention 情况:
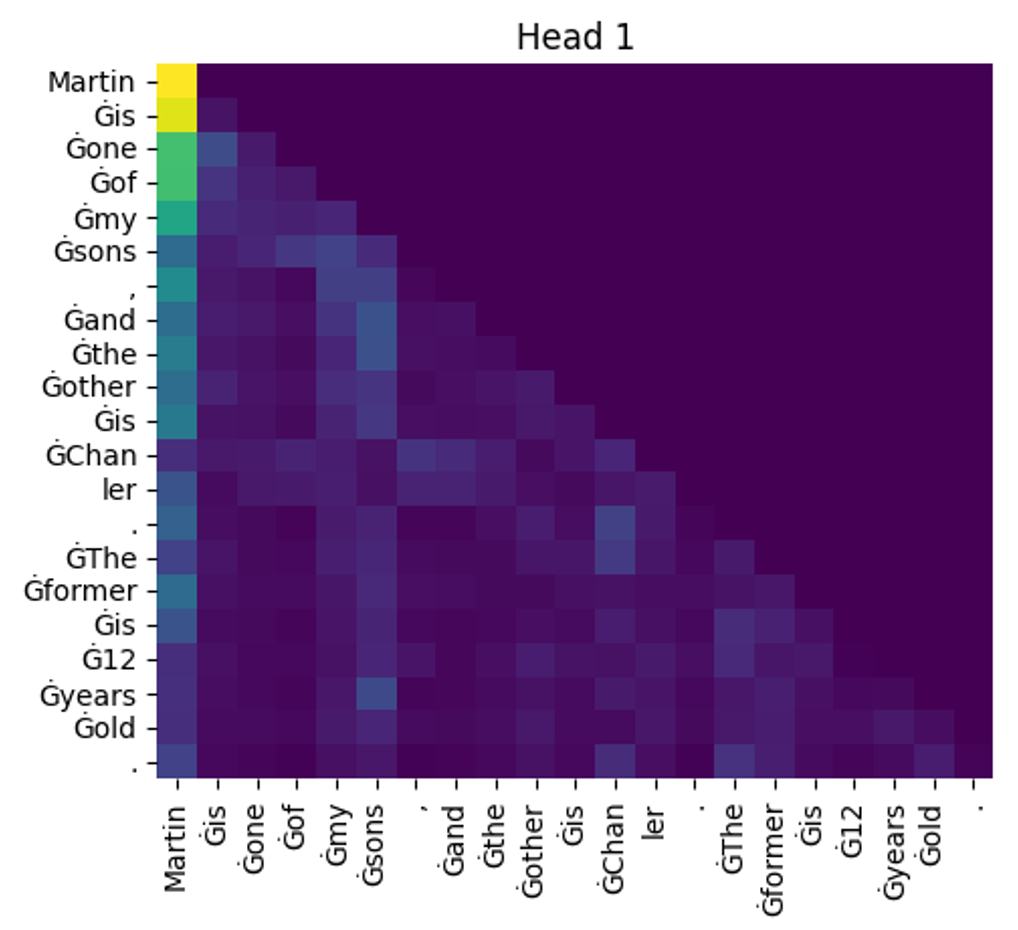
- 这句话总计有21个token,所以这是一个21×21的矩阵
- 这里是“masked self-attention”,所以矩阵的右上半区都是 “0” 。
- 在GPT2中,一共12层,每层12个“头”,所以一共有“144”个类似的矩阵
- \(W^Q \,, W^K \,, W^V \) 的维度都是768×64,所以粗略的估计这部分的参数量就超过2000万,具体的:
768*64*3*144 = 21,233,664
7. Multi-Head Attention
7.1 Scaled Dot-Product Attention
以前面小结“预处理”中的 X 为例,Attention Score Matrix 就有如下的计算公式:
$$
\begin{aligned}
\text{Attention Score Matrix} & = \text{softmax}(\frac{QK^T}{\sqrt{d}}) \\
& = \text{softmax}(\frac{XW^Q(XW^K)^T}{\sqrt{d}})
\end{aligned}
$$
最终的 Attention 计算如下:
$$
\begin{aligned}
\text{Attention}(Q,K,V) & = \text{softmax}(\frac{QK^T}{\sqrt{d}})V \\
& = \text{softmax}(\frac{XW^Q(XW^K)^T}{\sqrt{d}})XW^V
\end{aligned}
$$
7.2 Multi-Head Attention
上述的“Attention”在论文“Attention Is All You Need”称为“Scaled Dot-Product Attention”。更进一步的在论文中提出了“Multi-Head Attention”(经常被缩写为“MHA”)。对应的公式如下(来自原始论文):
$$
\begin{aligned}
\text{MultiHead}(Q, K, V) & = \text{Concat}(\text{head}_1, \dots, \text{head}_h)W^O \\
\text{where} \quad \text{head}_i & = \text{Attention}(QW_i^Q, KW_i^K, VW_i^V)
\end{aligned}
$$
更完整的解释,可以参考原始论文。这里依旧以前文的示例来说明什么是MHA。
在本文第4章“Self-Attention”中,较为详细的介绍了相关的计算(即模型的推理过程)。在示例中,一共有12个“Token”,在进入 Attention 计算时经过位置编码、正则化后,12个“Token”向量组成矩阵“X”,这里的“X”的 shape 为 12 x 768,通常使用符号 \(l \times d \) 或者 \(l \times d_{model} \) 表示。最终输出的 Contextual Embedding 也是 \(l \times d_{model} \) 的一组表示12个 Token 向量,这是每个向量相比最初的输入向量,则融合上下文中其他词语的含义。在一个多层的模型中,这组向量则可以作为下一层的输入。
在“Multi-Head Attention”其输入、输出与“Self-Attention”一样,都是 \(l \times d_{model} \) 。但是,对于最终输出的 \(l \times d_{model} \) 的向量/矩阵,在 MHA 中则分为多个 HEAD 各自计算其中的一部分,例如,一共有 \(d_{model} \) 列,那么则分别有 \(h \) 个HEAD,每个 HEAD 输出其中的 \(\frac{d_{model}}{h} \) 列。在上述示例中,供有12个HEAD,即 \(h=12 \),模型维度为768,即\(d_{model} = 768 \),所以每个HEAD,最终输出 \(64 = \frac{d_model}{h} = \frac{768}{12} \) 列。即:
$$
\begin{aligned}
\text{where} \quad \text{head}_i & = \text{Attention}(QW_i^Q, KW_i^K, VW_i^V)
\end{aligned}
$$
然后由12个 Head 共同组成(concat)要输出的 Contextual Embedding,并对此输出做了一个线性变换\(W^O \)。即:
$$
\begin{aligned}
\text{MultiHead}(Q, K, V) & = \text{Concat}(\text{head}_1, \dots, \text{head}_h)W^O
\end{aligned}
$$
7.3 Self Attention vs MHA
Self Attention
Multi Head Attention
7.4 Multi-Head Attention 小结
- “Multi-Head Attention” 与 经典“Attention” 有着类似的效果,但是有着更好的表现性能
- “Multi-Head Attention” 与 经典“Attention” 有相同的输入,相同的输出
8. Attention 数学计算示意图
如下的图片,半可视化的展示了在GTP2中,某一个HEAD中Attention的计算。
9. 全流程数学计算
完整的计算,就是一个“forward propagation”或者叫“inference”的过程,这里依旧以上述的提示词“It’s very hot in summer. Swimming is”,并观察该提示词在 GPT2 模型中的第一个Layer、第一个Head中的计算。完成的代码可以参考:Attention-Please.ipynb
9.1 Token Embedding 和 Positional Embedding
Token Embedding
+
Positional Embedding
|------------ ----------------------------------- ------------------------------- ------------------------------
| Token | | wte[:3] (word token embedding) | | wpe[:3](word positional e..)| | wte [:3] + wpe [:3] |
|------------ ----------------------------------- ------------------------------- ------------------------------
|It | | [0.039, -0.0869, 0.0662 ,...] | | [-0.0188, -0.1974, 0.004 ] | | [0.0202, -0.2844,0.0702 ] |
|âĢ | | [-0.075, 0.0948, -0.0034,...] | | [0.024, -0.0538, -0.0949] | | [-0.051, 0.041, -0.0982] |
|Ļ | | [-0.0223, 0.0182, 0.2631 ,...] | | [0.0042, -0.0848, 0.0545 ] | | [-0.0181,-0.0666,0.3176 ] |
|s | | [-0.064, -0.0469, 0.2061 ,...] | | [-0.0003, -0.0738, 0.1055 ] | | [-0.0643,-0.1207,0.3116 ] |
|Ġvery | | [-0.0553, -0.0348, 0.0606 ,...] | + | [0.0076, -0.0251, 0.127 ] | = | [-0.0477,-0.0599,0.1876 ] |
|Ġhot | | [0.0399, -0.0053, 0.0742 ,...] | | [0.0096, -0.0339, 0.1312 ] | | [0.0495, -0.0392,0.2054 ] |
|Ġin | | [-0.0337, 0.0108, 0.0293 ,...] | | [0.0027, -0.0205, 0.1196 ] | | [-0.031, -0.0098,0.149 ] |
|Ġsummer | | [0.0422, 0.0138, -0.0213,...] | | [0.0025, -0.0032, 0.1174 ] | | [0.0448, 0.0106, 0.0961 ] |
|. | | [0.0466, -0.0113, 0.0283 ,...] | | [-0.0012, -0.0018, 0.111 ] | | [0.0454, -0.0131,0.1394 ] |
|ĠSw | | [0.0617, 0.0373, 0.1018 ,...] | | [0.0049, 0.0021, 0.1178 ] | | [0.0666, 0.0395, 0.2196 ] |
|imming | | [-0.1385, -0.1774, -0.0181,...] | | [0.0016, 0.0062, 0.1004 ] | | [-0.1369,-0.1711,0.0823 ] |
|Ġis | | [-0.0097, 0.0101, 0.0556 ,...] | | [-0.0036, 0.0175, 0.1068 ] | | [-0.0133,0.0275, 0.1623 ] |
|------------ ----------------------------------- ------------------------------- ------------------------------
9.2 Normalize
即,将每一个token的embedding 进行正规化,将其均值变为0,方差变为1
Token | X norm[:3] (12 x 768)
--------------------------------------------
It | [ 0.0129, -0.1104, -0.0317,...]
âĢ | [-0.0530, 0.0588, -0.1290,...]
Ļ | [-0.0170, -0.0242, 0.1639,...]
s | [-0.0754, -0.0842, 0.1842,...]
Ġvery | [-0.0566, -0.0280, 0.0953,...]
Ġhot | [ 0.0587, -0.0086, 0.1073,...]
Ġin | [-0.0391, 0.0209, 0.0731,...]
Ġsummer | [ 0.0532, 0.0397, 0.0181,...]
. | [ 0.0553, 0.0152, 0.0579,...]
ĠSw | [ 0.0807, 0.0691, 0.1216,...]
imming | [-0.1528, -0.1249, -0.0017,...]
Ġis | [-0.0175, 0.0605, 0.0880,...]
9.3 Attention 层的参数矩阵
\(W^Q\,,W^K\,,W^V \)
W^Q [:3] shape (768 x 64) W^K [:3] shape (768 x 64) W^V [:3] shape (768 x 64)
------------------------------------- -------------------------------- --------------------------------
[-0.4738, -0.2614, -0.0978, ...] | [ 0.3660, 0.0771, 0.2226, ...] [ 0.1421, 0.0329, -0.0667, ...]
[ 0.0874, 0.1473, 0.2387, ...] | [-0.4380, -0.1446, -0.4717, ...] [ 0.0162, -0.0633, -0.0636, ...]
[ 0.0039, 0.0695, 0.3668, ...] | [ 0.1237, 0.0174, 0.1181, ...] [ 0.0229, -0.0828, 0.0437, ...]
[ 0.2215, -0.1884, -0.0141, ...] 64 [-0.2247, 0.0148, -0.1859, ...] [-0.0106, 0.0070, 0.0565, ...]
[-0.0947, 0.1678, -0.0143, ...] rows [-0.2001, -0.1052, -0.1743, ...] [ 0.0416, 0.0938, -0.1792, ...]
... | ... ...
[-0.4100, -0.1924, -0.2400, ...] | [,0.1567, 0.2664, 0.1851, ...] [-0.0341, 0.0034, 0.0203, ...]
------------------------------------- -------------------------------- --------------------------------
|<------- columns: 768 ------->| |<------- columns: 768 ------->| |<------- columns: 768 ------->|
9.4 矩阵 Q K V的计算
\(Q = XW^Q \)
\(K = XW^K \)
\(V = XW^V \)
Q [:3] shape (12 x 64) K [:3] shape (12 x 64) V [:3] shape (12 x 64)
------------------------------------- --------------------------------- --------------------------------
[ 0.4207, -0.9178, 0.1760, ...] | [ -1.4202, 1.6791, 0.9837, ...] [ 0.0452, 0.0628, 0.1463, ...]
[ 0.7757, 0.2485, 0.7349, ...] | [ -2.5320, 2.2932, 1.5592, ...] [-0.1361, 0.1379, 0.0150, ...]
[ 0.4481, 0.0206, -0.0825, ...] | [ -2.2571, 2.7764, 1.8401, ...] [ 0.0039, -0.1295, -0.0311, ...]
[ 0.9500, 0.1481, 0.3469, ...] 12 [ -2.4322, 3.1454, 2.0600, ...] [-0.0391, 0.0581, 0.0511, ...]
[ 0.4989, -0.4376, 0.1678, ...] rows [ -3.5428, 2.1485, 2.0414, ...] [ 0.0963, 0.3563, -0.1477, ...]
... | ... ...
[ 0.4429, -1.1997, 0.5611, ...] | [ -2.2559, 2.0384, 2.2542, ...] [ 0.2759, -0.2783, 0.3240, ...]
------------------------------------- --------------------------------- --------------------------------
|<------- columns: 64 ------->| |<------- columns: 64 ------->| |<------- columns: 64 ------->|
9.5 计算 Attention Score
\(\text{Attention Score} \)
\(= \frac{QK^T}{\sqrt{d}} \)
|---------------------------------------------------------------------------------------------|
| | Attention Score Matrix shape (12 x 12) |
| Token |-------------------------------------------------------------------------------------|
| | It âĢ Ļ s Ġvery Ġhot Ġin Ġsummer . ĠSw imming Ġis |
|-------|-------------------------------------------------------------------------------------|----
|It | [ 0.14, -1.53, -1.45, -1.71, -1.69, -1.74, -2.36, -2.27, -2.37, -1.33, -0.58, -2.40]| |
|âĢ | [ 0.70, -0.93, -1.72, -1.02, -1.52, -2.24, -1.90, -2.19, -1.63, -2.13, -1.66, -2.14]| |
|Ļ | [-0.60, -1.81, -1.99, -1.96, -2.57, -1.84, -1.62, -2.04, -0.98, -1.18, -2.23, -2.25]| |
|s | [-0.46, -1.33, -1.60, -2.65, -2.24, -1.99, -2.89, -1.44, -2.05, -2.77, -2.09, -2.74]| |
|Ġvery | [ 0.29, -1.42, -1.77, -1.15, -0.94, -1.14, -1.81, -1.04, -1.77, -2.13, -0.60, -0.82]| |
|Ġhot | [ 0.03, -0.68, -0.59, -0.95, -1.78, -0.10, -0.95, -0.14, -1.32, -0.57, 0.06, -1.07]| 12
|Ġin | [-0.71, -1.72, -1.53, -2.18, -1.67, -1.93, -3.41, -1.69, -2.74, -1.89, -1.17, -2.02]| rows
|Ġsummer| [-0.34, -1.49, -1.35, -1.31, -1.12, -0.89, -1.49, -1.11, -1.51, -1.15, -1.45, -1.20]| |
|. | [-0.89, -1.73, -2.67, -2.80, -2.45, -2.37, -4.39, -2.33, -4.42, -2.73, -1.82, -3.21]| |
|ĠSw | [-0.05, -1.15, -1.76, -1.15, -1.68, -0.74, -1.15, -1.35, -1.36, -1.29, -0.43, -1.51]| |
|imming | [-0.02, -1.65, -0.87, -0.35, -1.18, -0.65, -0.33, -1.25, -0.38, -1.68, -2.15, -1.08]| |
|Ġis | [-0.97, -2.03, -2.56, -2.94, -1.96, -2.71, -4.07, -2.46, -3.51, -2.68, -1.88, -2.99]| |
|-------|-------------------------------------------------------------------------------------|----
|<-------------------------------- columns: 12 -------------------------------------->|
9.6 计算 Masked Attention Score
\(\text{Masked Attention Score} \)
\(= \frac{QK^T}{\sqrt{d}} + \text{mask} \)
|---------------------------------------------------------------------------------------------|
| | Masked Attention Score Matrix shape (12 x 12) |
| Token |-------------------------------------------------------------------------------------|
| | It âĢ Ļ s Ġvery Ġhot Ġin Ġsummer . ĠSw imming Ġis |
|-------|-------------------------------------------------------------------------------------|----
|It | [ 0.14, -inf, -inf, -inf, -inf, -inf, -inf, -inf, -inf, -inf, -inf, -inf]| |
|âĢ | [ 0.70, -0.93, -inf, -inf, -inf, -inf, -inf, -inf, -inf, -inf, -inf, -inf]| |
|Ļ | [-0.60, -1.81, -1.99, -inf, -inf, -inf, -inf, -inf, -inf, -inf, -inf, -inf]| |
|s | [-0.46, -1.33, -1.60, -2.65, -inf, -inf, -inf, -inf, -inf, -inf, -inf, -inf]| |
|Ġvery | [ 0.29, -1.42, -1.77, -1.15, -0.94, -inf, -inf, -inf, -inf, -inf, -inf, -inf]| |
|Ġhot | [ 0.03, -0.68, -0.59, -0.95, -1.78, -0.10, -inf, -inf, -inf, -inf, -inf, -inf]| 12
|Ġin | [-0.71, -1.72, -1.53, -2.18, -1.67, -1.93, -3.41, -inf, -inf, -inf, -inf, -inf]| rows
|Ġsummer| [-0.34, -1.49, -1.35, -1.31, -1.12, -0.89, -1.49, -1.11, -inf, -inf, -inf, -inf]| |
|. | [-0.89, -1.73, -2.67, -2.80, -2.45, -2.37, -4.39, -2.33, -4.42, -inf, -inf, -inf]| |
|ĠSw | [-0.05, -1.15, -1.76, -1.15, -1.68, -0.74, -1.15, -1.35, -1.36, -1.29, -inf, -inf]| |
|imming | [-0.02, -1.65, -0.87, -0.35, -1.18, -0.65, -0.33, -1.25, -0.38, -1.68, -2.15, -inf]| |
|Ġis | [-0.97, -2.03, -2.56, -2.94, -1.96, -2.71, -4.07, -2.46, -3.51, -2.68, -1.88, -2.99]| |
|-------|-------------------------------------------------------------------------------------|----
|<-------------------------------- columns: 12 -------------------------------------->|
9.7 计算 Softmax Masked Attention Score
\(\text{Softmax Masked Attention Score} \)
\(= \text{softmax}(\frac{QK^T}{\sqrt{d}} + \text{mask}) \)
|-------------------------------------------------------------------------------------|
| | Softmax Masked Attention Score Matrix shape (12 x 12) |
| Token |-----------------------------------------------------------------------------|
| | It âĢ Ļ s Ġvery Ġhot Ġin Ġsummer . ĠSw imming Ġis |
|-------|-----------------------------------------------------------------------------|
|It | [1.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00]| |
|âĢ | [0.84 0.16 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00]| | V [:3] shape (12 x 64)
|Ļ | [0.65 0.19 0.16 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00]| | --------------------------------
|s | [0.54 0.23 0.17 0.06 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00]| | [ 0.0452, 0.0628, 0.1463, ...]
|Ġvery | [0.54 0.10 0.07 0.13 0.16 0.00 0.00 0.00 0.00 0.00 0.00 0.00]| | [-0.1361, 0.1379, 0.0150, ...]
|Ġhot | [0.29 0.14 0.16 0.11 0.05 0.25 0.00 0.00 0.00 0.00 0.00 0.00]| 12 [ 0.0039, -0.1295, -0.0311, ...]
|Ġin | [0.36 0.13 0.16 0.08 0.14 0.11 0.02 0.00 0.00 0.00 0.00 0.00]| rows [-0.0391, 0.0581, 0.0511, ...]
|Ġsummer| [0.26 0.08 0.09 0.10 0.12 0.15 0.08 0.12 0.00 0.00 0.00 0.00]| | [ 0.0963, 0.3563, -0.1477, ...]
|. | [0.40 0.17 0.07 0.06 0.08 0.09 0.01 0.10 0.01 0.00 0.00 0.00]| | ...
|ĠSw | [0.27 0.09 0.05 0.09 0.05 0.14 0.09 0.07 0.07 0.08 0.00 0.00]| | [ 0.2759, -0.2783, 0.3240, ...]
|imming | [0.19 0.04 0.08 0.14 0.06 0.10 0.14 0.06 0.13 0.04 0.02 0.00]| | --------------------------------
|Ġis | [0.30 0.10 0.06 0.04 0.11 0.05 0.01 0.07 0.02 0.05 0.12 0.04]| | |<------- columns: 64 ------->|
|-------|-----------------------------------------------------------------------------|
|<-------------------------------- columns: 12 ------------------------------>|
9.8 计算 Contextual Embeddings
\(\text{Contextual Embeddings} \)
\(= \text{softmax}(\frac{QK^T}{\sqrt{d}} + \text{mask})V \)
Token | Contextual Embedding (12 x 768)
--------------------------------------------
It | [ 0.0452, 0.0628, 0.1463,...]
âĢ | [ 0.0153, 0.0752, 0.1247,...]
Ļ | [ 0.0034, 0.0464, 0.0923,...]
s | [-0.0082, 0.0464, 0.0801,...]
Ġvery | [ 0.0218, 0.1029, 0.0621,...]
Ġhot | [ 0.0327, 0.0892, 0.0409,...]
Ġin | [ 0.0249, 0.0964, 0.0329,...]
Ġsummer | [ 0.0583, 0.1195, 0.0068,...]
. | [ 0.0334, 0.1100, 0.0366,...]
ĠSw | [ 0.0086, 0.0846, 0.0074,...]
imming | [-0.0049, 0.0841, -0.0339,...]
Ġis | [ 0.0410, 0.0706, 0.0077,...]
10. 其他
上述流程详述了 LLM 模型中 Attention 计算的核心部分。也有一些细节是省略了的,例如,
- 在GPT2中,“线性变换”是有一个“截距”(Bias)的,所以也可以称为一个“仿射变换”,即在一个线性变换基础上,再进行一次平移;
- 在GTP2中,Attention计算都是多层、多头的,本文主要以Layer 0 / Head 0 为例进行介绍;
- 在生成最终的“Contextual Embeddings”之前,通常还需要一个MLP层(全连接的前馈神经网络)等,本文为了连贯性,忽略了该部分。
总结一下,本文需要的前置知识包括:矩阵基本运算、矩阵与线性变换、SVD 分解/特征值特征向量、神经网络基础、深度学习基础等。
注
- [1] 多头注意情况可能是 \(d \times \frac{d}{h} \)
- [2] 对于满秩方阵也可以使用“特征值/特征向量”的方式去理解
- [3] 在 GPT 2 中,一个 Attention 层的计算,会分为“多头”去计算;并在计算后,还会再经过一个 MLP 层

Leave a Reply