Word Embedding 的可解释性探索

1 TL;DR
2 概述
3 寻找某个关心的方向
4 原理解释
5 更深层次的理解
6 补充说明

这大概是一个有趣、也略深刻的发现。

Word Embedding是比较抽象的，但是这些抽象背后是一些“具象”的含义的，本文通过一些简单的计算（变换）来将Embedding的某些维度/属性具象化。具体的，本文展示了在Embedding空间中，找到一个代表“动物”属性的方向。感兴趣的话，可以通过这个简单的方法，找到你感兴趣的属性方向。

TL;DR

通常，在某个具体的Word Embedding实现中，先给出一组具有“共同属性”的词语，然后计算这组词语Embedding向量的平均方向，就可以代表这个“共同属性”。

例如，找到一组“动物”，然后对这些词语的Embedding向量计算平均方向，那么这个方向就是“动物”这个属性的方向。

概述

如果你也尝试过去理解 Embedding 各个维度的含义的话，大概都听过这样一种说法：Embedding每个维度可以理解为这个词语的某种属性，例如，“性别属性”、“皇室相关度”等，这是最为经典的man - woman = king - queue的例子中的一些解释。

当你真的拿到一个词语的 Embedding 的时候，它可能有768维，但是，似乎没有一个维度有上述的清晰的属性含义。而实际上，这些属性含义是确实存在的，只是这些属性方向并不存在于“标准基”的方向上。

那如果存在，我们应该如何找到这个方向呢？本文展示并验证了一个非常简单的方法，让你快速找到某种属性的方向，并且进行一些验证。从而可以大大加深对于 Embedding 的理解。

寻找某个关心的方向

这里展示了以寻找“动物”属性方向为例，展示如何寻找并验证该方向。

列出最具代表性的词语

我们这样考虑这个问题，如果有一个方向表示一个词语的“动物”属性，那么这个方向会是哪个方向？这里以all-MiniLM-L6-v2模型提供的Sentence Embedding为例，我看看如何找到该Embedding所处的向量空间中最可能代表“动物”属性的方向是哪个？具体的方法描述如下：

首先，找到被认为最典型的与“动物”属性相关的词语$ n $个，这里取$ n=50 $
然后计算上述$ n $个词语的平均方向 avg_vector，该方向则认为要寻找的方向

这里，给出的50个动物如下：

animals = [
    "tiger", "lion", "elephant", "giraffe", "zebra",
    "rhinoceros", "hippopotamus","crocodile", "monkey",
    "panda", "koala", "kangaroo","whale", "dolphin",
    "seal", "penguin", "shark", "snake", "lizard",
    "turtle", "frog", "butterfly", "bee", "ant", "eagle",
    "sparrow", "pigeon", "parrot", "owl", "duck", "chicken",
    "dog", "cat", "pig", "cow", "sheep", "horse", "donkey",
    "rabbit", "squirrel", "fox", "wolf", "bear", "deer",
    "hedgehog", "bat", "mouse", "chameleon", "snail", "jellyfish"
]

计算Embedding的平均方向

该平均方向，即为我们要寻找的“动物”属性方向。

animals_embeddings = model.encode(animals)
avg_animals_embeddings = np.mean(animals_embeddings, axis=0)

验证该方向

再选取两组词，一组认为是与“动物”非常相关的词，另一组则是与动物无关的词语。然后分别计算这两组词语在上述方向avg_vector的投影值。观察投影值，是否符合预期。

这里选择的两组词语分别是：

与动物非常相关的：”Camel”, “Gorilla”, “Cheetah”
与动物无关的：”Dream”, “Chair”, “Mathematics”

计算投影并可视化

具体的程序如下：

animals_words    = ["Camel", "Gorilla", "Cheetah"]
un_animals_words = ["Dream", "Chair", "Mathematics"]

for word_list in (animals_words,un_animals_words):
    projection_scores = np.dot(model.encode(word_list),
                              avg_animals_embeddings)
    results.update({word: score for word,
                    score in zip(word_list, projection_scores)})

for word, score in results.items():
    print(f"'{word}': {score:.4f}")
print(np.round(avg_animals_embeddings[:10], 4))

投影结果为：

'Camel': 0.3887
'Gorilla': 0.4186
'Cheetah': 0.3797
'Dream': 0.2450
'Chair': 0.2823
'Mathematics': 0.1972

在实数轴上绘制上述两组词语的投影：

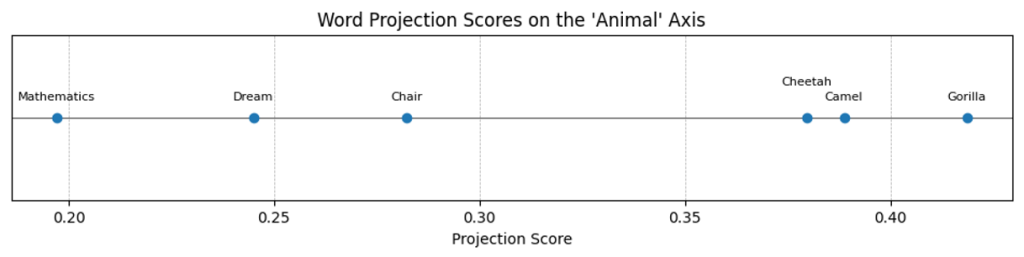
非常明显的可以看到，上述的avg_vector方向某种程度上代表了一个词语的“动物”属性：即与动物属性相关的词语在该方向的投影大，无关的词语在该方向的投影小。

原理解释

概述

事实上，一组词语Embedding的“平均向量”（centroids of word embeddings），则某种程度的代表这组词语的“语义中心”。如果这组词有某些共性，那么这个平均向量，则可能就是这个共性的代表。

在上述的例子中，刻意地给出的一组词语都是“动物”名称。那么，这个“平均向量”则比较有可能代表了这个向量空间中的“动物”属性。

数学推导

这样考虑这个问题：现在给出的 $ n $ 个向量 $ \alpha_1, \dots , \alpha_n $，找出一个单位向量 $ \xi $ 使得 $ n $ 个向量在 $ \xi $ 向量方向上的投影值的和最大。

这里取 $ \bar{\alpha} = \frac{\sum\limits_{i=1}^{n}\alpha_i}{n} $

目标函数 $ S = \sum\limits_{i=1}^{n}(\alpha_i \cdot \xi ) = \sum\limits_{i=1}^{n}(\alpha_i) \cdot \xi = n \bar{\alpha} \cdot \xi = n \| \bar{\alpha}\| \| \xi \| \cos\theta $

这里 $ n $、$ \bar{\alpha} $都是给定值，而 $ \| \xi \| = 1 $，所以这里 $ \cos\theta $ 取最大值时，上述的目标函数 $ S $ 取最大值。

即：$ \theta = 0 $ 时， $ S $ 取最大值。即当 $ \xi $ 与 $ \bar{\alpha} $ 方向相同时，即 $ \xi = \frac{\bar{\alpha}}{\|\bar{\alpha}\|} $ ，所有向量的投影值的和最大。

投影计算

太久不碰线性代数了，对于基本运算都不是很熟悉了。向量 $ \alpha $ 在 $ \beta $ 方向上的投影长度，计算公式如下：

$$ proj = \frac{\alpha \cdot \beta}{\|\beta\|} $$

证明比较简单，这里不再赘述。

向量的平均方向与主成分方向

当给出一组向量，面对上述问题，比较容易联想到这组向量的“主成分分析”的第一个维度。那么，上述的平均向量和主成分分析的第一个维度有什么关系呢？回答是：没有太大的关系。

可以看下面三个图：

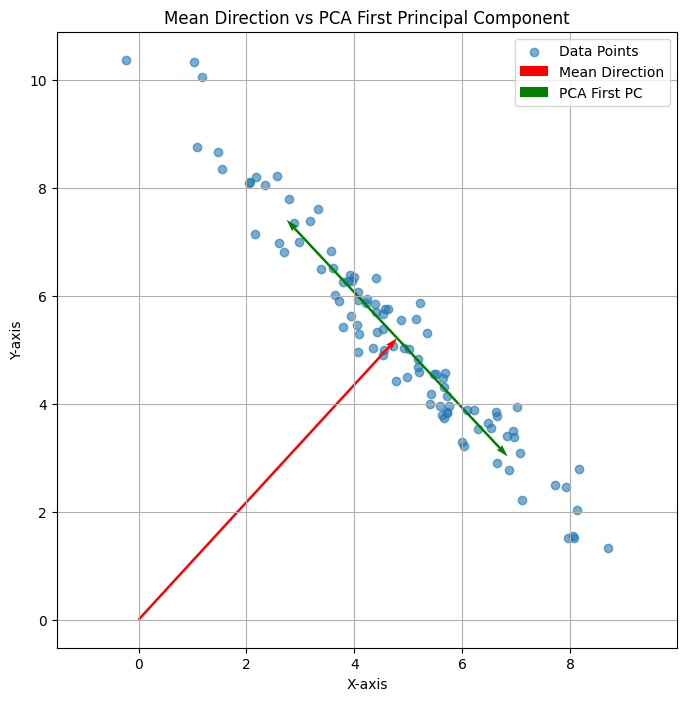
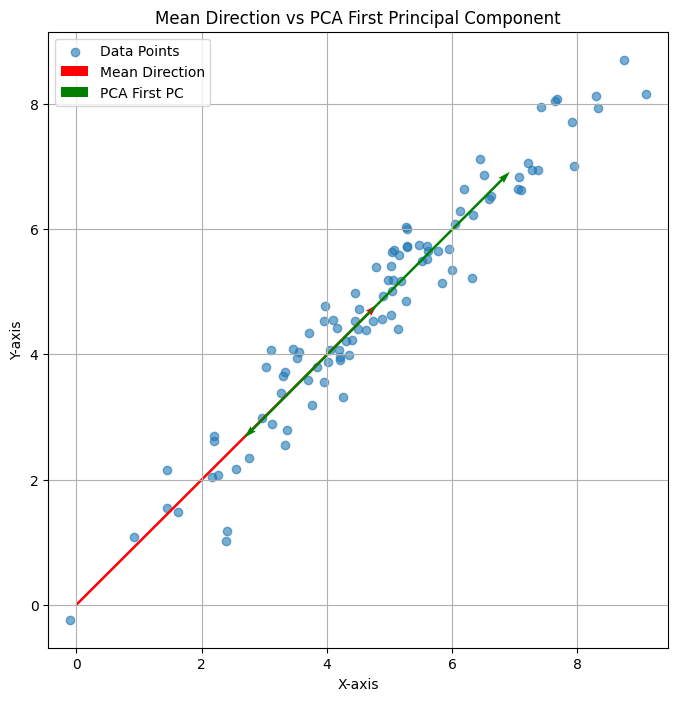
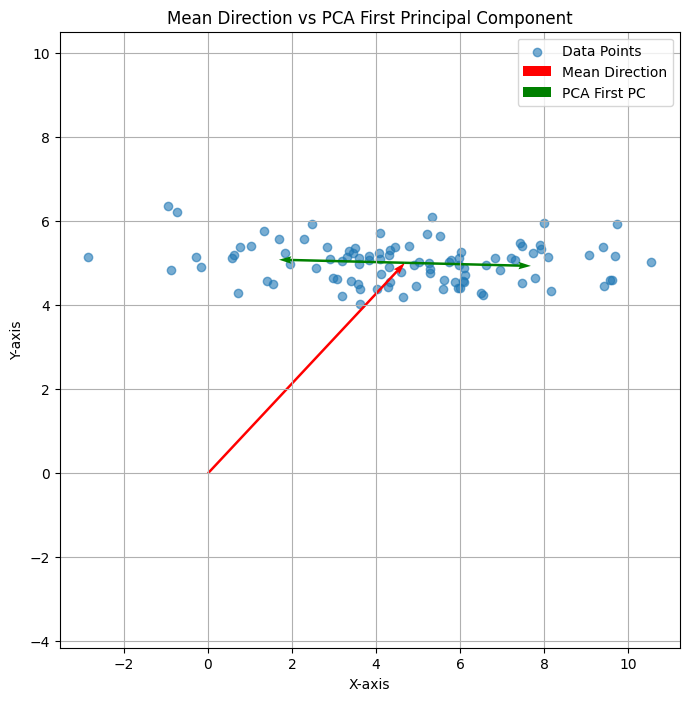
上述三个二维平面中的点的平均方向均为红色，即(1,1)；但是PCA的第一方向则各有不同，有时候与平均向量相同、有时候垂直，有时候相交。总之是没什么关系。

可以看到，平均向量时在当前的“基”下计算获得。而主方向分析的方向，则首先就与原点没有关系。

更深层次的理解

现在的Embedding算法，都是基于现实世界语料库训练而来，反应了人类认知中“语言”与现实世界的对应关系。而在人类的认知中，这个世界是有“维度”的，最为直白的例子就是：我们会将词语划分“褒义词”、“贬义词”。此外，可能还有：动物性、情感强烈度、词性等。那么，在人类认知中这种“认知”有多少个维度呢？这其实是未知的，而各种Embedding算法则是在尝试使用量化的方式描述这些维度。

但是，在实际训练出的各种Embedding实现，例如一个768维的Embedding，其单位向量方向，不太可能是上述的人类“认知”维度。如果把训练出来的Embedding的单位向量记为：$ \alpha_1, \dots , \alpha_n $，而把人类认知的维度记为： $ \beta_1, \dots , \beta_n $ 。

那么，则存在一个过渡矩阵 $T$，可以实现上述向量空间基的变换。

可是，现实世界没有那么理想。Embedding空间确实给出了一组正交基，但是人类认识却很难寻找这样的正交基，例如“动物”属性的词语，可能会带有“情感”属性，例如，“虎狼之词”等，都带有某种情感属性。

虽然，认知很难找到正交的“基”，但是找到某个具体的属性方向，则可以使用本书的方法。这正是本文所描述方法的局限性和价值所在。

补充说明

本文中，所说的Word Embedding，通常是指Sentence Embedding中的Token Embedding。在这里，无需区分两者。
实际的情况更加复杂，例如本文中的“动物”属性，只是这些词所代表的“动物”属性。什么是真正的“动物”属性，并不存在这样的精确概念。人类语言中的“动物”是一个抽象的，并没有数字化、数学化的精确定义。
完整的实现代码，参考：embedding_research_01.py。

orczhou.com