目录
DiskANN 是较为常见的向量数据库搜索算法,作者通过“贪婪搜索”和“健壮性剪枝”(“RobustPrune”)来构建一个“低直径”的图,从而实现高性能的向量搜索。这里的“低直径”很好的保障了点与点之间非常高效(只需要少数几条)完成搜索。“RobustPrune”则是构建低直径的“Vamana”图的关键步骤。本文通过计算推导、示例与试验的方式,来看看“RobustPrune”如何实现“低直径”图的构建,而这也正是 DiskANN 算法的核心之一。
1. RobustPrune 概述
论文中的原始描述如右图。
可以这样理解:在找到 \(p \) 的若干“邻居”后(邻居集合记为 \(N_{out}(p) \) ),由于“边”(出度)数量有限(这里是 \(R \) ),故需要进行“剪枝”,那么这里的“剪枝”方法即为“RobustPrune”:
- 在 \(N_{out}(p) \) 中找出距离 \(p \) 最近的点,记为 \(p^{*} \)
- 需要“剪枝”时,将满足下列条件的点都“剪掉”:
- \(\alpha \cdot d(p^{*},p’) \le d(p,p’) \)

在初次看到,表达式 \(\alpha \cdot d(p^{*},p’) \le d(p,p’) \) 的时候,是比较难理解其背后的用意的,本文则较为详细以分析、推导、“试验”的方式介绍该公式在图构建过程中所取的效果。
2. 二维空间的示例
这里以二维空间为例,以一个具体的场景来观察 RobustPrune 的效果。具体的,将上述的“剪枝”操作描述为如下的数学形式:
2.1 “剪枝”区域计算
在二维坐标系中有 \(P = (0,0) \, A = (2,0) \) ,考虑该集合:
$$
\mathscr{L} = \{ X | \frac{d(X,P)}{d(X,A)} \le \alpha \quad \text{and} \quad d(X,A) < d(X,P) \}
$$
即,在 RobustPrune 中落入该区域的点,将被剪枝。
这里 \(\alpha \) 是一个常数,且 \(\alpha \gt 1 \) 。 假设, \(\mathscr{L} \) 中的点 \(X\) 坐标是 \((x,y) \),那么推导 \(x \, y \) 需要满足怎样的限制条件。
在上述的“数学”问题中,点 \(P = (0,0) \) 即为论文算法中的 \(p \),点 \(A \) 即为论文算法中距离 \(p \) 点最近的邻居 \(p^{*} \)。问题中的 \(x \, y \) 限制提交,即为论文中的“剪枝”条件。
根据“简单”的数学推导(详细推导可以参考附录,为了连续性这里暂不详述),有如下结果,即坐标 \((x , y) \) 需满足如下条件:
$$
(x-\frac{2\alpha^2}{\alpha^2-1})^2 + y^2 \le \frac{4\alpha^2}{(\alpha^2-1)^2}
$$
可以看到,这是一个以 \(\frac{2\alpha}{\alpha^2 -1} \) 为半径,以 \((\frac{2\alpha^2}{\alpha^2-1},0) \) 为圆心的圆内部区域(包括边缘)。
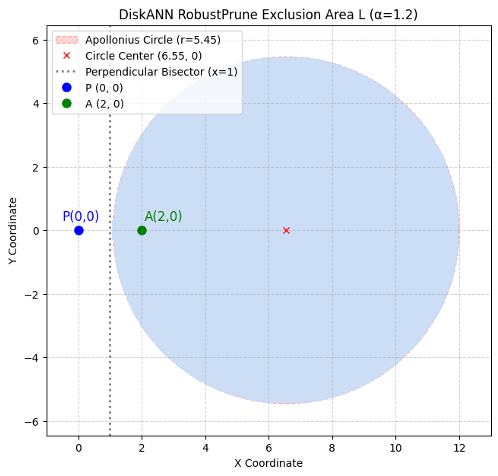
更为具体的,取 \(\alpha = 1.2 \),则在坐标系中,该区域为右图。
即,当 \(P \) 点、 \(A \) 点确定时,落入右侧图形中阴影部分的点,均会被“剪枝”。
2.2 实际“剪枝”区域
更为一般的,如果在平面中任意去一些点,也有类似的结论。其对应的“剪枝圆”(有的地方会称为“遮蔽空间),则有如下的形式:
考虑右图中, \(A \) 为距离 \(P \) 最近的邻居,那么看看点 \(B \)、\(C \) 是否会被遮蔽。
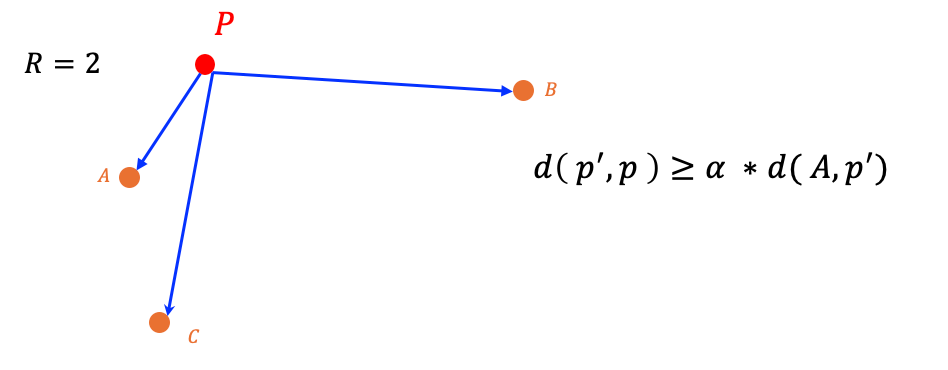
与上述推导类似的,可以计算出对应的“剪枝圆”如右图阴影部分,因为 \(C \) 点恰好落在该区域(且又因为邻居数量超过最大出度),故 \(C \) 将被从邻居中删除。
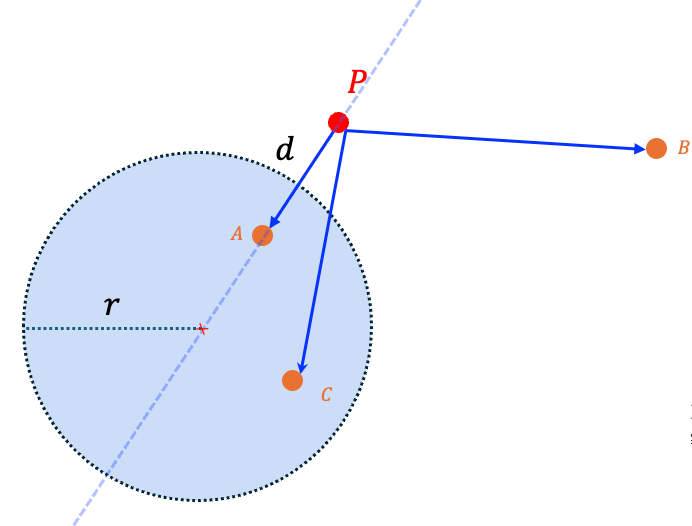
这就是 RobustPrune 在二维空间的效果。更进一步的,为什么这样进行剪枝就可以保障“低直径”呢?
3. “剪枝”、不“剪枝”的对比
为了进一步加深对 RobustPrune 效果的理解,我们考虑这样的问题:在一个 Vamana 图的构建过程中,使用 RobustPrune 进行“剪枝”和不使用该方法剪枝,构建的图会有什么不同?
在进行正式的试验验证之前,我们有理由这样去考虑:因为“出度” \(R \) 是固定的值,将距离 \(A \) 很近的点从候选邻居中删除,可以避免某些区域邻居过于集中,并将该位置预留给距离 \(P \) 远一些的邻居,这可能会有利于降低图的直径。
上述理解,即为 RobustPrune 的直觉建立的比较核心的理解。
为了更好的理解上述内容,并验证上述“直觉”,这里通过程序随机生成30点,并尝试构建 Vamana 图,在构建过程中对比使用 RobustPrune 剪枝和不进行剪枝,看看两种方式构建的图有什么差异。
3.1 剪枝、不剪枝对比图
具体的实现程序参考:Vamana Graph.ipynb。程序中,先生成 30 个随机的点,如 Figure 1;然后分别使用带有“剪枝”、没有“剪枝”的算法,生成图,如 Figure 2、Figure3。
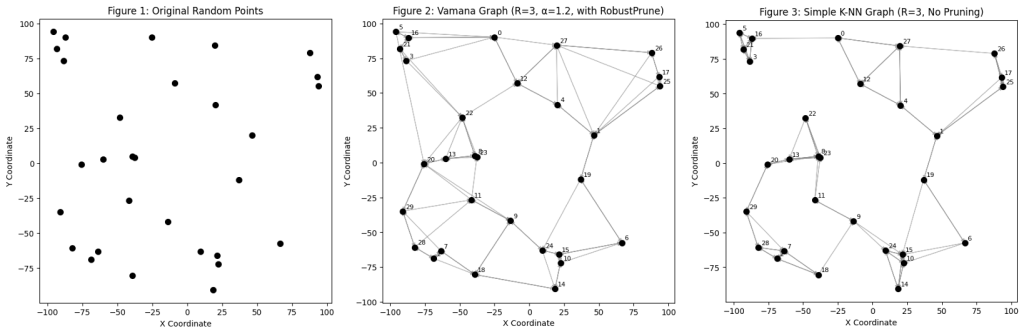
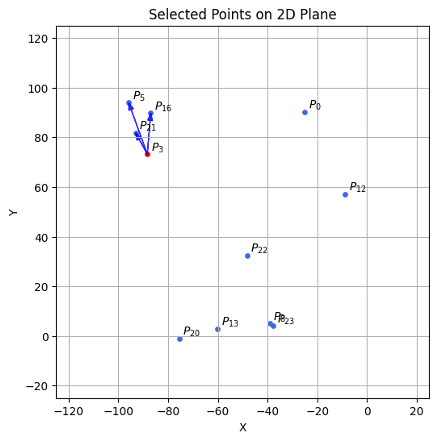
这里可以较为直观的看到,因为这里的“出度” \(R = 3 \) 是固定的,点“3”和点“22”,在剪枝和不剪枝的情况下,两个点之间的距离相差非常大,这也最终导致图的“直径”相差很大。
4. 拆解 RobustPrune “剪枝”过程
这里以点“3”,记为 \(P_3 \), 为例,看看RobustPrune “剪枝”是如何进行的。
首先,在该示例中使用“最近”初始化的方法(而不是随机初始化),即对于每一个点,例如这里的 \(P_3 \) ,初始其“出度”(out degree)候选邻居为距离其最近的10个点,即
$$ N_{out}(p) = \{ P_{21}\,P_{16}\,P_5 \, P_{22}\, P_0 \, P_{20}\, P_{13}\, P_{12}\, P_8\, P_{23} \} $$
这里考虑的欧式距离,故最近的点为 \(P_{21} \)。
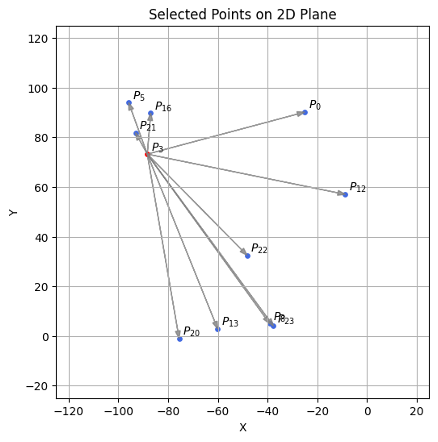
4.1 考虑RobustPrune剪枝
在进行RobustPrune剪枝时,点 \(P_5 \, P_{16} \)处于点\(P_{21} \)的遮蔽区域,故进行剪枝。最终保留了点:\( N_{out}(p) = \{ P_{21} \, P_{22}\, P_0 \} \)
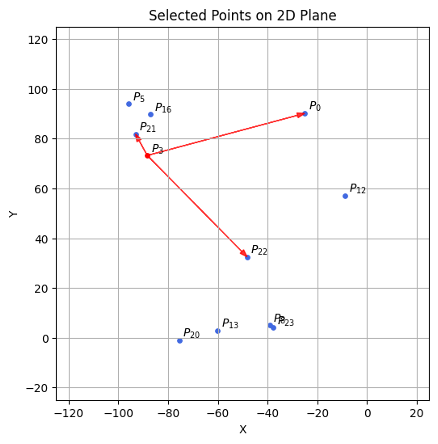
4.2 不考虑剪枝
不考虑“剪枝”,又因为这里最大出度\(R=3 \),故保留距离 \(P_3 \) 最近的三个点,则为:\( N_{out}(p) = \{ P_{5} \, P_{16}\, P_{21} \} \)
4.3 剪枝区域
在上述的示例中,我们可以绘制考虑 \(P_3 \) 时,取 \(\alpha = 1.2 \)时,剪枝所涉及的遮蔽区域如下,即落到该区域内的点(除了最近的 \(P_{21} \) ),都将被剪枝,如右图。
并且,因为最大出度 \(R = 3 \),在剩余的点中,再额外选取两个最近的点保留,这里即为:\(\{ P_0 \, P_{22} \} \)。
所以,经过RobustPrune剪枝,最终 \(\{ P_3 \} \) 保留的“出度”邻居点集为
$$
N_{out}(P_3) = \{ P_{21} \, P_{0} \, P_{22} \}
$$
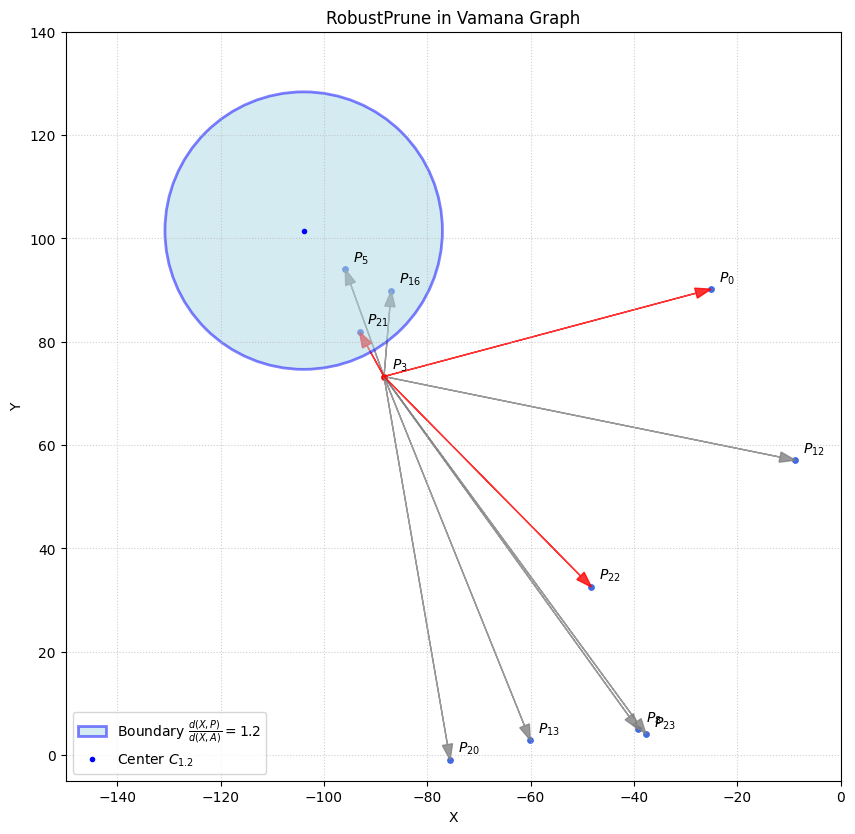
可以看到,经过剪枝,在构建 \(P_3 \) 的出度邻居时,在最大出度限制为 \(R=3 \) 时,很好的避免了图邻居的“聚集”,从而最终减低了整个图的直径,就有了上述的最终构建效果:

5. 最后
这里给出的示例是二维的,在这个场景下,高维扩展并没有太大的不同。从构建“直觉”的角度,这里给出示例已经足够。对于更高维的场景,如果感兴趣的,可以自己进行推导。
附录:数学推导
这里,\(P = (0,0) \, A = (2,0) \),再根据剪枝公式有:
$$
\begin{aligned}
\frac{d(X,P)}{d(X,A)} & \ge \alpha \\
\frac{\sqrt{x^2+y^2}}{\sqrt{(x-2)^2+y^2}} & \ge \alpha \\
\frac{x^2+y^2}{(x-2)^2+y^2} & \ge \alpha^2 \\
x^2+y^2 & \ge \alpha^2((x-2)^2+y^2) \\
x^2+y^2 & \ge \alpha^2x^2 -4\alpha^2 x + 4\alpha^2 + \alpha^2 y^2 \\
0 & \ge x^2 – \frac{4\alpha^2 x}{(\alpha^2-1)} + \frac{4\alpha^2}{(\alpha^2-1)} + y^2 \\
0 & \ge (x- \frac{2\alpha^2}{(\alpha^2-1)})^2 – (\frac{2\alpha^2}{(\alpha^2-1)})^2 + \frac{4\alpha^2}{(\alpha^2-1)} + y^2 \\
(x- \frac{2\alpha^2}{(\alpha^2-1)})^2 + y^2 & \le (\frac{2\alpha^2}{(\alpha^2-1)})^2 – \frac{4\alpha^2}{(\alpha^2-1)}\\
(x- \frac{2\alpha^2}{(\alpha^2-1)})^2 + y^2 & \le (\frac{2\alpha}{\alpha^2-1})^2 \quad \blacksquare
\end{aligned}
$$

Leave a Reply