目录
如果要理解大模型内部是如何工作的,良好的数学基础是必须的,而线性代数又是所有这些的基础。例如我们来看 \(\text{Attention} \) 机制中的如下问题。
1. 为什么要重温线性代数
考虑第 \(j \) 个 \( \text{Layer} \) 中的第 \( i \) 个 \( \text{Head} \) ,则有如下的计算(为了简化,下述的角标省略了 \( \text{Layer} \) 部分):
$$
\begin{aligned}
Q_i &= XW_i^Q \\[0.3em]
K_i &= XW_i^K \\[0.3em]
\text{Therefore:} \\[0.3em]
\text{Attention Score}_i &= Q_iK_i^T \\[0.3em]
&= XW_i^Q(XW_i^K)^T \\[0.3em]
&= XW_i^Q\big((W_i^K)^T X^T\big) \\[0.3em]
&= XW_i^Q(W_i^K)^T X^T \\[0.3em]
&= X\big(W_i^Q (W_i^K)^T\big) X^T \\[0.3em]
\text{Let:} \quad \\[0.3em]
W_i^{QK} &= W_i^Q (W_i^K)^T \\[0.3em]
\text{Therefore:} \\[0.3em]
\text{Attention Score}_i &= XW_i^{QK} X^T \\[0.3em]
\end{aligned}
$$
注:上述的推导使用矩阵的一些简单特性,包括转置计算、结合律等。其中,在开源的GPT2模型中,\(W_i^Q \,, W_i^K \) 都是 \(64 \times 768 \)的矩阵。
这里一个简单、又不太简单的问题是:那为什么每一个 \( \text{Head} \) 中不使用一个权重 \( W_i^{QK} \) 就可以了?这个问题从我第一次看明白 \( \text{Attention} \) 的计算后,困扰了我一会儿,直到重温了线性代数,才算是理解了上述的计算。
大学时学习线性代数学得非常痛苦,而现在带着问题再去看这本书,竟然花了两个晚上就看完了。这里对里面的基本概念和结论做个梳理,以更好的理解什么是“线性变换”、与矩阵的关系是什么、如何研究一个线性变换或矩阵的性质等。
本系列主要以介绍线性代数的“直觉”为主,不会做任何证明,为了更好的阐述“直觉”,甚至牺牲了很多的数学严谨,看客也需要从构建“直觉”与“联系”的角度阅读。本文的阅读前提是已经有一定的线性代数的基础、也对神经网络/LLM技术有一定了解,那么本文则尝试通过较小的篇幅去构建两者的联系,看看如何使用线性代数的技术去研究神经网络的中的问题。
2. 线性代数讨论的主要问题
通常“线性代数”课程会从 \(n\) 元一次线性方程组引入,并使用行列式理论,去较为彻底的回答如何解决 \(n\) 元一次线性方程组。更进一步的,为了更好/更完整的研究 \(n\) 元一次线性方程组的“解空间”,则需要引入一个新的研究对象:“向量空间”。而向量空间本身所具备的普遍性,已经远超出 \(n\) 元一次线性方程组本身。而后,“向量空间”、“线性变换”就变成了新的研究对象,因为现实问题中,我们经常会尝试通过“线性变换”来洞察向量空间中向量的关系。
是不是感觉上面描述漏了什么?是的,漏了“矩阵”。无论是讨论 \(n\) 元一次线性方程组还是“向量空间”或“线性变换”,矩阵都是“核心”工具。这个工具“核心”或者说重要到什么程度呢?甚至很多问题,只需要研究清楚对应“矩阵”的特性,原来的问题就研究清楚了。所以,你会注意到,线性代数的书中,几乎全都在介绍“矩阵”的各种特性。
而各种 \( \text{Embedding} \) 就可以理解为是在最为典型的欧氏空间中的向量。
3. \(n \) 元一次方程组的解
线性代数通常都会以解“\( n \)元一次方程组”为切入点,这个问题看似很简单,但是最终要完全讨论清楚,则需要很多篇幅。这也是“线性代数”前半部分比较枯燥的原因。整体上来看,关于“\( n \)元一次方程组”的解需要讨论清楚几个问题:
- (a) \( n \)元一次方程组的解是否存在?
- (b) 如果存在,如何求解
- (c) 如果解不存在,充要条件是什么
- (d) 如果有解,那么所有的解如何表达
在探讨上述问题的时候,先是引入了“行列式”、“矩阵”的概念与理论,并通过矩阵的“初等变换”实现对上述问题的求解。这里涉及到的概念延伸出了:
- (a) 矩阵的初等变换
- (b) 矩阵的秩等
这里我们列举一些主要的结论(并不做推倒,推倒过程还是非常复杂的,这也正是线性代数书比较枯燥的原因之一)。这里考虑如下的线性方程组:
$$
a_{11}x_1 + a_{12}x_2 + \cdots + a_{1n}x_n = b_1, \\
a_{21}x_1 + a_{22}x_2 + \cdots + a_{2n}x_n = b_2, \\
\quad\vdots \\
a_{m1}x_1 + a_{m2}x_2 + \cdots + a_{mn}x_n = b_m.
$$
结论: 线性方程组有解的充分必要条件是:它的系数矩阵与增广矩阵有相同的秩。
结论: 线性方程组系数矩阵和增广矩阵的秩都是\( r \),方程组的未知数的个数是\( n \),如果:
- \( r = n \) 则线性方程组有唯一解
- \( r < n \) 则线性方程组有无穷组解
上述两个定理较为彻底的回答了解存在性的问题。那么,解的公式化表达是怎样的呢?为了略微简化问题,这里考虑仅考虑\( n \)个方程、\( n \)个未知数,且解唯一的情况:
$$
\begin{cases}
a_{11}x_1 + a_{12}x_2 + \cdots + a_{1n}x_n = b_1, \\
a_{21}x_1 + a_{22}x_2 + \cdots + a_{2n}x_n = b_2, \\
\quad\vdots \\
a_{n1}x_1 + a_{n2}x_2 + \cdots + a_{nn}x_n = b_n
\end{cases}
\quad\Longleftrightarrow\quad
\begin{bmatrix}
a_{11} & a_{12} & \cdots & a_{1n} \\
a_{21} & a_{22} & \cdots & a_{2n} \\
\vdots & \vdots & \ddots & \vdots \\
a_{n1} & a_{n2} & \cdots & a_{nn}
\end{bmatrix}
\begin{bmatrix}
x_1 \\ x_2 \\ \vdots \\ x_n
\end{bmatrix}
=
\begin{bmatrix}
b_1 \\ b_2 \\ \vdots \\ b_n
\end{bmatrix}
$$
形式化的解,则可以由两种方式给出:
使用矩阵的表达:
$$
\vec{x} = A^{-1}\vec{b}
$$
“克莱默法则”(Cramer’s rule / formula):
$$
x_1 = \frac{D_1}{D},x_2 = \frac{D_2}{D},\dots , x_n = \frac{D_n}{D},
$$
注意:上述的两种表达,无论哪种,限制条件都非常苛刻,即要求:矩阵\( A \)可逆或者行列列式\(D \neq 0\),当然,这两个条件式等价的。并且,这里的\(D\)也经常写作:\( det(A) \)。
4. 矩阵基础与部分结论
虽然是为了求解线性方程组才引入矩阵的,但很快就会意识到,对矩阵本身特性的研究有着更为广泛的应用。
首先,在定义了矩阵的运算之后,很快就会有一些矩阵的运算律。例如,加法的结合律、交换律、分配律等。这里,矩阵的乘法是重点,且略微复杂一些:
- 首先,首先矩阵的乘法是不满足交换律的
- 很幸运,结合律和分配律都是满足的
- 再次,对于转置运算,是满足如下形式的:\( (AB)^T = B^TA^T \)
结论: 线性方程组的初等变换,对应着三个初等变换矩阵:\( P_{ij} \)、\( D_i(k) \)、\( T_{ij}(k) \),且这三个初等变换矩阵都是可逆的。
结论: 一个\( m \times n\)的矩阵\( A \)总是可以通过初等变换化为以下形式的矩阵:
$$ \bar{A} = \begin{bmatrix}
I_r & O_{r,\,n-r} \\
O_{m-r,\,r} & O_{m-r,\,n-r}
\end{bmatrix} $$
这里,\(I_r\)是\( r \)阶单位矩阵,\(O_{st}\)表示\( s\times t\)的零矩阵,\( r \)等于矩阵\(A\)的秩。
结论:\(n \) 阶矩阵\( A \)可逆,当且仅当\( A \)的秩等于\( n \)。
如何求解矩阵的逆:有了这些结论,那么对于一个可逆矩阵要求其逆矩阵,则可以有些办法:即对一个矩阵实施一系列的初等变换,将其变为单位矩阵。而同时,在开始的时候,就将所有的这些初等变换作用在一个单位矩阵上。最后,当原矩阵变为单位矩阵的时候,后面的单位矩阵就变成原矩阵的逆了。
结论: 两个矩阵乘积的秩,不大于任何一个矩阵的秩。特别的,如果有一个矩阵是可逆的,则乘积的秩则等于另一个矩阵的秩。
结论: 一个矩阵的行空间的维数等于列空间的维数,等于这个矩阵的秩。
5. 向量空间
到目前为止,前面的线性方程组的解,还有一些问题没有彻底回答(例如,解空间的描述),在回答这个问题之前,我们需要先了解一下“向量空间”。“向量空间”的严格定义是有些枯燥的,这里暂时把“向量空间”的限制为大家所熟悉的、最为典型的“ \(n \) 维欧氏空间”。
5.1 基
要描述一个向量空间中的元素,则首先需要一组基(坐标)。在\(n\)维欧氏空间,最为常见的一组基,即为多个“垂直”(“正交”)的单位向量,即:
$$ \begin{align}
\alpha_1 &= (1,0,\dots) \\
& \vdots \\
\alpha_i &= (\dots,0,1,0,\dots) \\
& \vdots \\
\alpha_n &= (0,\dots,1)
\end{align}
$$
在二维平面空间中,则为:\( \alpha_1 = (1,0) \quad \alpha_2 = (0,1)\);三维空间则为:\( \alpha_1 = (1,0,0) \quad \alpha_2 = (0,1,0) \quad \alpha_3 = (0,0,1)\)。
既然有“正交”基,那么当然有不那么“正交”的基,而此类“基”则是更为普遍的。事实上,更为普遍的,任何 \( n \) 个线性无关的向量都可以作为向量空间的基。
5.2 线性相关与线性无关
考虑一组向量\( \alpha_1,\dots , \alpha_n \),如果当且仅当所有\( a_i = 0 \quad i=1,\dots,n\)时如下的等式才成立:
$$ a_1\alpha_1 + a_2\alpha_2 + \dots + a_n\alpha_n = 0 $$
那么,就说 这组向量 \( \alpha_1,\dots , \alpha_n \) 是线性无关的。反之,则称这组向量是线性相关的。
或者这么说,对于一组线性无关的向量\( \alpha_1,\dots , \alpha_n \):任何一个向量都不能用剩余的向量做“线性表示”。
5.3 一些重要的结论
结论:设\( \{ \alpha_1,\dots , \alpha_n \}\)是向量空间\( V \)的一组基,那么\( V \)空间中的每一个向量都可以唯一的表示为这组基的线性组合。这个线性组合的系数,就叫“坐标”(注:相对于这组基)。
结论:\( W_1 \)、\( W_2 \)是\( V \)的有限子空间,那么有:
$$ dim(W_1+W_2) = dim(W_1) + dim(W_2) – dim(W_1\cap W_2) $$
结论:\( n \)维向量空间中,任意\( n \)个线性无关的向量都可以取做基。
6. 线性变换与矩阵
6.1 概述
“线性变换”是指向量空间中一类特殊的映射 \( \sigma : R^n \to R^m \) ,需要满足条件是:
- \( \sigma(\xi + \eta) = \sigma(\xi) + \sigma(\eta) \)
- \( \sigma(a\xi) = a\sigma(\xi) \)
“线性变换” 描述了向量空间之间的映射。后续所有的内容大概都是围绕此而展开,后续所有的内容都会尝试通过各种方式将 “线性变换” 的特性研究清楚。这里写出部分结论,后面再慢慢展开:
- 线性变换之下,原点保持不变。即 \( \sigma( \vec{0} ) = \vec{0} \)
- 几何意义下,通常,线性变换包括了:旋转、镜像、拉伸/压缩(特别的,有时候会压缩到零)、剪切
为了研究清楚一个线性变换上述的特点,通常需要选取一组“基”,然后使用这组“基”的“坐标”来描述空间中的点,进而再描述对应的线性变换。最为常见的基为“正交单位基”。
从方法上来看,研究清楚“线性变换”最为关键的是研究清楚对应的“变换矩阵”。所以,“线性代数”的核心后面就变成了对矩阵特性的研究,但是,也不要忘记了初衷,否则很快就迷失了。
6.2 线性变换
我在大学期间对于线性变换、矩阵有什么作用,是完全没有概念的。所以对于他们的特性研究也没有掌握的很深,基本上是停留在能够把一些联系题做对这个层面。而现在,注意线性变换的广泛应用之后,尝试去理解去本质之后,就会寻根问底的去理解清楚什么是线性变换、什么是矩阵。这里再次说说我的理解。
在一个向量空间中,最为常见的是 \(n \) 维欧氏空间,会有很多的向量,例如每个 Embedding 就可以理解是在一个线性空间中,“线性变换”表述了是空间中的一类映射,该映射满足上述“小结2.1”中的两个要求,即原点依旧到原点、映射保持所谓的“线性”(例如,向量和的映射等于映射的和等)。
在一个向量空间中,一个线性变换就是一个符合一定条件的映射。与向量空间的基的选取是没有关系的。自此,与矩阵也是没有关系的。所以,线性变换本身是更为底层、更为基础的概念。
6.3 欧氏空间的线性变换与矩阵
现在我们把问题限定在 \(n \) 维欧氏空间中。那么,这时候,我们如何描述一个线性变换呢?是的,就是“基”与“矩阵”。
通常,\(n \) 维欧氏空间,我们会先选取一组基,然后使用一个矩阵去描述这个线性变换。并且非常幸运的,一旦这组基 选定了,这个矩阵是唯一的。
结论:在\(n \) 维欧氏空间(这个条件似乎可以去掉)中,对于线性变换 \(\sigma \),如果选定一组“基”,那么就存在唯一的“矩阵”描述该线性变换。
上述的结论,是比较明显的。我们考虑对于线性变换中的上述选定的基向量 \(\alpha_i,\quad \text{where } i = 1,\ldots,n \),线性变换将其映射到 \(\beta_i,\quad \text{where } i = 1,\ldots,n \),那么根据“基”的基本性质,对于这里的任何 \(\beta_i \)都可以表示成\(\alpha_i \)的线性组合,所有的这些系数构成的矩阵,就是上述描述的唯一的“矩阵”。具体的:
$$
\begin{aligned}
\beta_1 &= a_{11}\alpha_1 + a_{21}\alpha_2 + \cdots + a_{n1}\alpha_n \\[0.5em]
\beta_2 &= a_{12}\alpha_1 + a_{22}\alpha_2 + \cdots + a_{n2}\alpha_n \\[0.5em]
&\ \vdots \\[0.5em]
\beta_n &= a_{1n}\alpha_1 + a_{2n}\alpha_2 + \cdots + a_{nn}\alpha_n
\end{aligned}
$$
即:
$$
\begin{aligned}
\begin{bmatrix}
\beta_1 & \beta_2 & \cdots & \beta_n
\end{bmatrix}
=
\begin{bmatrix}
\alpha_1 & \alpha_2 & \cdots & \alpha_n
\end{bmatrix}
\begin{bmatrix}
a_{11} & a_{12} & \cdots & a_{1n} \\
a_{21} & a_{22} & \cdots & a_{2n} \\
\vdots & \vdots & \ddots & \vdots \\
a_{n1} & a_{n2} & \cdots & a_{nn}
\end{bmatrix}
\end{aligned}
$$
即在这个线性变换\(\sigma \) 在选定基 \(\alpha_i,\quad \text{where } i = 1,\ldots,n \) 对应的矩阵为:
$$
\begin{aligned}
A =
\begin{bmatrix}
a_{11} & a_{12} & \cdots & a_{1n} \\
a_{21} & a_{22} & \cdots & a_{2n} \\
\vdots & \vdots & \ddots & \vdots \\
a_{n1} & a_{n2} & \cdots & a_{nn}
\end{bmatrix}
\end{aligned}
$$
从这段简洁的“证明”(或“说明”)来看,我们很自然有如下结论,根据空间中的“基”的选取不同,我们会得到不同的矩阵。因为我们反复会提到,我们经常会通过研究矩阵的特性来研究线性变换。那么,同一个线性变换在不同的“基”下的不同“矩阵”,很自然的能够想到,这些“矩阵”是有某些共性的,是的,我们称这些矩阵为“相似矩阵”,相关特性,暂不展开。
7. 特征向量与特征值
7.1 为什么
为什么我们需要关注“特征值与特征向量”呢?为什么我们要去了解奇异值分解(SVD)呢?
原因是“线性变换”是一个映射,是非常抽象的。而特征值 、特征向量、SVD分解可以把线性变换最为关键的特性,以非常“直观”的形式表达出来。当然,这里的“直观”并不是简单意义上能够一眼就看出什么来,事实上,“线性变换”本身就有很强的抽象性,这里的“直观”只是相对的,是否直观,完全依赖于各位看客自己的“悟性”了 。
特征向量的基本定义:如果有 \( \sigma(\xi) = \lambda \xi \) ,那么这里的 \( \xi \) 就是特征向量,对应的 \(\lambda \) 就是对应的特征值。
要想真正说清楚特征向量与特征值是需要非常多篇幅的,而且关于对特征向量的理解对于理解线性变化也是非常关键的,所以,建议花些时间较为系统的做一些理解。如果你已经建立的基础概念,这里的一篇文章可能是帮助你增强一些理解:特征向量与特征值。
7.2 关于对特征向量的理解
完整的讨论特征向量与特征值是复杂的,这里将其限定在一些较为简单的情况,作为一个入门。我们这里考虑最为简单的情况,即对于一个 \(n \times n \)的矩阵,其秩为 \(n \),并且在计算特征值时,有 \(n \) 是不重复的实数解,即没有任何根式重根。如果,恰好 \( n = 2 \)这大概是最为简单的情况了,不过理解这种情况,再进一步拓展,则学习曲线会平滑很多。
我们来看一个实例,在二维空间中,在标准基下,我们有如下的线性变换矩阵:
$$
W = \begin{bmatrix}
2 & 1 \\
1 & 2
\end{bmatrix}
$$
根据上述特征向量特征值的定义进行求解,我们可以有如下的特征值与特征向量:
- \( \lambda_1 = 3 \) 特征向量 \( (1,1) \)
- \( \lambda_2 = 1 \) 特性向量 \( (-1,1) \)
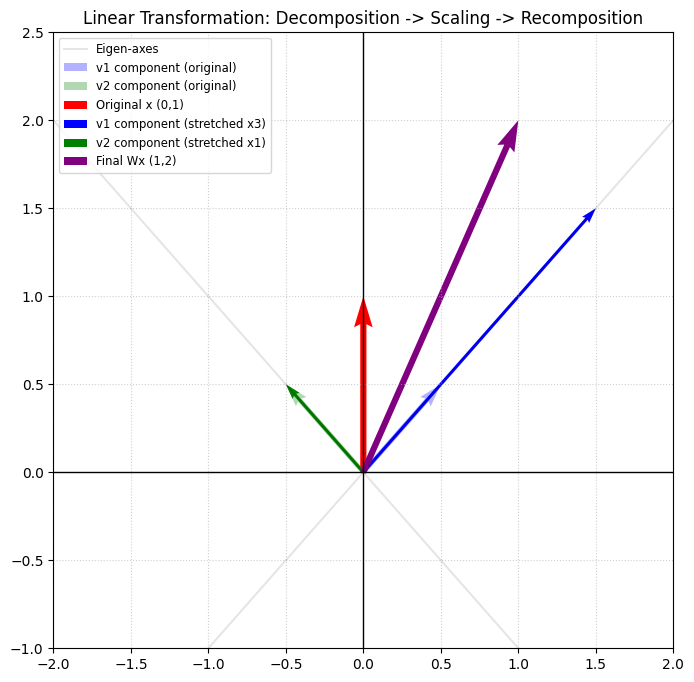
从特征向量角度理解线性变换:那么上述的矩阵A对应的线性变换 \(\sigma \) 有如下特性,在这个二维空间任何向量 \(\beta \),都可以分解(投影)为上述两个特征向量方向的向量: \(\beta_1 \,, \beta_2 \),且有:\(\beta = \beta_1 + \beta_2 \)。那么,则有:\(\sigma(\beta) = \lambda_1 \beta_1 + \lambda_2 \beta_2 \)。即,这个线性变换可以这样描述:先将任何向量沿着特征向量方向分解,然后再按照特征值的大小进行拉伸或压缩,然后再把向量合并起来。
上述的解释,可以对照着右图去理解。特征向量分别为 \((1,1) \) 和 \((-1,1) \) ,即图中浅绿色、浅蓝色方向。该矩阵作用在向量 \((0,1) \) 上,即图中的红色向量。先将红色向量沿着浅绿色、浅蓝色方向分解,然后按照特征值进行拉伸,即图中的绿色、蓝色向量,最后合并为图中的紫色最终向量。
上述的场景是线性变换中,最为简单的一类。而实际的线性变换,则更为复杂,可能还涉及到对于向量的旋转、镜像、剪切等变换。关于更多场景可以自己探索,或者阅读相关书籍,也可以看看这篇文章中的更多直观的例子:特征值与特征向量。
“特征向量”可以很好的帮助理解“方阵”变换,还有一类变换时非方阵的情况,通常这时候可以借助于奇异值分解的方式去理解,关于奇异值分解可以参考:奇异值分解–深度学习的数学基础。
8. 一些补充说明
初等的线性代数核心部分大概是这些内容,出于完整性的考虑,可以再进一步了解“Jordan 块”相关的内容,从而把相关理论补充完整,这里不再详述。
如果再回到最初的线性方程组解的问题,我们这里就可以回答最后一个问题:对于一个线性方程组,如果有解,那么所有的解空间是怎样的?
结论:如果方程组的系数矩阵的秩为\( r \),那么解空间的维度为\( n-r \)。解空间的“基”则可以通过初等变换求得。这里不再详述。
9. 再看看前面的问题
$$
\begin{aligned}
\text{Attention Score}_i = XW_i^{QK} X^T \quad \text{where} \,,W_i^{QK} = W_i^Q (W_i^K)^T
\end{aligned}\tag{1}
$$
$$
\text{Attention Score}_i = Q_iK_i^T = XW_i^Q(XW_i^K)^T \tag{2}
$$
在上面的计算(1) 和 计算(2),那么在模型中训练 \(W_i^{QK} \) 和 在模型中训练单独训练 \(W_i^Q \,,W_i^K \) 是否是等价的?
答案是否定的。
这里以 GTP2 模型为例,原因在于如果单独训练 \(W_i^{QK} \) ,那么这个矩阵的秩,则很可能是 768 ;而单独训练 \(W_i^Q \,,W_i^K \),这两个矩阵的秩则一定小于 64,这两个矩阵的乘积的秩也一定是 64 (严格来说是小于等于)。所以最终训练获得的效果一定是不同的。当然,哪个更好,这倒不一定,但他们并不是等价的。
一般意义来说,使用 \(W_i^{QK} \) 可能有着更强的表达能力,只是意义没有那么明确,并且训练的参数要更多。

Leave a Reply