到目前为止，前面的线性方程组的解，还有一些问题没有彻底回答（例如，解空间的描述），在回答这个问题之前，我们需要先了解一下“向量空间”。“向量空间”的严格定义是有些枯燥的，这里暂时把“向量空间”的限制为大家所熟悉的、最为典型的“ \(n \) 维欧氏空间”。

1. 向量空间

1.1 基

要描述一个向量空间中的元素，则首先需要一组基（坐标）。在\(n\)维欧氏空间，最为常见的一组基，即为多个“垂直”（“正交”）的单位向量，即：

$$ \begin{align}
\alpha_1 &= (1,0,\dots) \\
& \vdots \\
\alpha_i &= (\dots,0,1,0,\dots) \\
& \vdots \\
\alpha_n &= (0,\dots,1)
\end{align}
$$

在二维平面空间中，则为：\( \alpha_1 = (1,0) \quad \alpha_2 = (0,1)\)；三维空间则为：\( \alpha_1 = (1,0,0) \quad \alpha_2 = (0,1,0) \quad \alpha_3 = (0,0,1)\)。

既然有“正交”基，那么当然有不那么“正交”的基，而此类“基”则是更为普遍的。事实上，更为普遍的，任何 \( n \) 个线性无关的向量都可以作为向量空间的基。

1.2 线性相关与线性无关

考虑一组向量\( \alpha_1,\dots , \alpha_n \)，如果当且仅当所有\( a_i = 0 \quad i=1,\dots,n\)时如下的等式才成立：

$$ a_1\alpha_1 + a_2\alpha_2 + \dots + a_n\alpha_n = 0 $$

那么，就说 这组向量 \( \alpha_1,\dots , \alpha_n \) 是线性无关的。反之，则称这组向量是线性相关的。

或者这么说，对于一组线性无关的向量\( \alpha_1,\dots , \alpha_n \)：任何一个向量都不能用剩余的向量做“线性表示”。

1.3 一些重要的结论

结论：设\( \{ \alpha_1,\dots , \alpha_n \}\)是向量空间\( V \)的一组基，那么\( V \)空间中的每一个向量都可以唯一的表示为这组基的线性组合。这个线性组合的系数，就叫“坐标”（注：相对于这组基）。

结论：\( W_1 \)、\( W_2 \)是\( V \)的有限子空间，那么有：

$$ dim(W_1+W_2) = dim(W_1) + dim(W_2) – dim(W_1\cap W_2) $$

结论：\( n \)维向量空间中，任意\( n \)个线性无关的向量都可以取做基。

2. 线性变换与矩阵

2.1 概述

“线性变换”是指向量空间中一类特殊的映射 \( \sigma : R^n \to R^m \) ，需要满足条件是：

• \( \sigma(\xi + \eta) = \sigma(\xi) + \sigma(\eta) \)
• \( \sigma(a\xi) = a\sigma(\xi) \)

“线性变换” 描述了向量空间之间的映射。后续所有的内容大概都是围绕此而展开，后续所有的内容都会尝试通过各种方式将 “线性变换” 的特性研究清楚。这里写出部分结论，后面再慢慢展开：

• 线性变换之下，原点保持不变。即 \( \sigma( \vec{0} ) = \vec{0} \)
• 几何意义下，通常，线性变换包括了：旋转、镜像、拉伸/压缩（特别的，有时候会压缩到零）、剪切

为了研究清楚一个线性变换上述的特点，通常需要选取一组“基”，然后使用这组“基”的“坐标”来描述空间中的点，进而再描述对应的线性变换。最为常见的基为“正交单位基”。

从方法上来看，研究清楚“线性变换”最为关键的是研究清楚对应的“变换矩阵”。所以，“线性代数”的核心后面就变成了对矩阵特性的研究，但是，也不要忘记了初衷，否则很快就迷失了。

2.2 线性变换

我在大学期间对于线性变换、矩阵有什么作用，是完全没有概念的。所以对于他们的特性研究也没有掌握的很深，基本上是停留在能够把一些联系题做对这个层面。而现在，注意线性变换的广泛应用之后，尝试去理解去本质之后，就会寻根问底的去理解清楚什么是线性变换、什么是矩阵。这里再次说说我的理解。

在一个向量空间中，最为常见的是 \(n \) 维欧氏空间，会有很多的向量，例如每个 Embedding 就可以理解是在一个线性空间中，“线性变换”表述了是空间中的一类映射，该映射满足上述“小结2.1”中的两个要求，即原点依旧到原点、映射保持所谓的“线性”（例如，向量和的映射等于映射的和等）。

在一个向量空间中，一个线性变换就是一个符合一定条件的映射。与向量空间的基的选取是没有关系的。自此，与矩阵也是没有关系的。所以，线性变换本身是更为底层、更为基础的概念。

2.3 欧氏空间的线性变换与矩阵

现在我们把问题限定在 \(n \) 维欧氏空间中。那么，这时候，我们如何描述一个线性变换呢？是的，就是“基”与“矩阵”。

通常，\(n \) 维欧氏空间，我们会先选取一组基，然后使用一个矩阵去描述这个线性变换。并且非常幸运的，一旦这组基 选定了，这个矩阵是唯一的。

结论：在\(n \) 维欧氏空间（这个条件似乎可以去掉）中，对于线性变换 \(\sigma \)，如果选定一组“基”，那么就存在唯一的“矩阵”描述该线性变换。

上述的结论，是比较明显的。我们考虑对于线性变换中的上述选定的基向量 \(\alpha_i,\quad \text{where } i = 1,\ldots,n \)，线性变换将其映射到 \(\beta_i,\quad \text{where } i = 1,\ldots,n \)，那么根据“基”的基本性质，对于这里的任何 \(\beta_i \)都可以表示成\(\alpha_i \)的线性组合，所有的这些系数构成的矩阵，就是上述描述的唯一的“矩阵”。具体的：

$$
\begin{aligned}
\beta_1 &= a_{11}\alpha_1 + a_{21}\alpha_2 + \cdots + a_{n1}\alpha_n \\[0.5em]
\beta_2 &= a_{12}\alpha_1 + a_{22}\alpha_2 + \cdots + a_{n2}\alpha_n \\[0.5em]
&\ \vdots \\[0.5em]
\beta_n &= a_{1n}\alpha_1 + a_{2n}\alpha_2 + \cdots + a_{nn}\alpha_n
\end{aligned}
$$

即：

$$
\begin{aligned}
\begin{bmatrix}
\beta_1 & \beta_2 & \cdots & \beta_n
\end{bmatrix}
=
\begin{bmatrix}
\alpha_1 & \alpha_2 & \cdots & \alpha_n
\end{bmatrix}
\begin{bmatrix}
a_{11} & a_{12} & \cdots & a_{1n} \\
a_{21} & a_{22} & \cdots & a_{2n} \\
\vdots & \vdots & \ddots & \vdots \\
a_{n1} & a_{n2} & \cdots & a_{nn}
\end{bmatrix}
\end{aligned}
$$

即在这个线性变换\(\sigma \) 在选定基 \(\alpha_i,\quad \text{where } i = 1,\ldots,n \) 对应的矩阵为：

$$
\begin{aligned}
A =
\begin{bmatrix}
a_{11} & a_{12} & \cdots & a_{1n} \\
a_{21} & a_{22} & \cdots & a_{2n} \\
\vdots & \vdots & \ddots & \vdots \\
a_{n1} & a_{n2} & \cdots & a_{nn}
\end{bmatrix}
\end{aligned}
$$

从这段简洁的“证明”（或“说明”）来看，我们很自然有如下结论，根据空间中的“基”的选取不同，我们会得到不同的矩阵。因为我们反复会提到，我们经常会通过研究矩阵的特性来研究线性变换。那么，同一个线性变换在不同的“基”下的不同“矩阵”，很自然的能够想到，这些“矩阵”是有某些共性的，是的，我们称这些矩阵为“相似矩阵”，相关特性，暂不展开。

3. 特征向量与特征值

3.1 为什么

为什么我们需要关注“特征值与特征向量”呢？为什么我们要去了解奇异值分解（SVD）呢？

原因是“线性变换”是一个映射，是非常抽象的。而特征值 、特征向量、SVD分解可以把线性变换最为关键的特性，以非常“直观”的形式表达出来。当然，这里的“直观”并不是简单意义上能够一眼就看出什么来，事实上，“线性变换”本身就有很强的抽象性，这里的“直观”只是相对的，是否直观，完全依赖于各位看客自己的“悟性”了 。

特征向量的基本定义：如果有 \( \sigma(\xi) = \lambda \xi \) ，那么这里的 \( \xi \) 就是特征向量，对应的 \(\lambda \) 就是对应的特征值。

要想真正说清楚特征向量与特征值是需要非常多篇幅的，而且关于对特征向量的理解对于理解线性变化也是非常关键的，所以，建议花些时间较为系统的做一些理解。如果你已经建立的基础概念，这里的一篇文章可能是帮助你增强一些理解：特征向量与特征值。

3.2 关于对特征向量的理解

完整的讨论特征向量与特征值是复杂的，这里将其限定在一些较为简单的情况，作为一个入门。我们这里考虑最为简单的情况，即对于一个 \(n \times n \)的矩阵，其秩为 \(n \)，并且在计算特征值时，有 \(n \) 是不重复的实数解，即没有任何根式重根。如果，恰好 \( n = 2 \)这大概是最为简单的情况了，不过理解这种情况，再进一步拓展，则学习曲线会平滑很多。

我们来看一个实例，在二维空间中，在标准基下，我们有如下的线性变换矩阵：

$$
W = \begin{bmatrix}
2 & 1 \\
1 & 2
\end{bmatrix}
$$

根据上述特征向量特征值的定义进行求解，我们可以有如下的特征值与特征向量：

• \( \lambda_1 = 3 \) 特征向量 \( (1,1) \)
• \( \lambda_2 = 1 \) 特性向量 \( (-1,1) \)

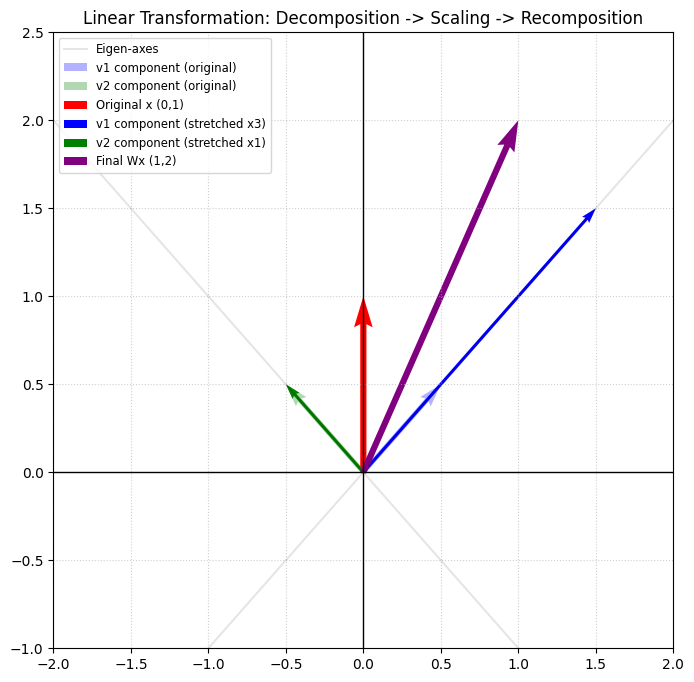
从特征向量角度理解线性变换：那么上述的矩阵A对应的线性变换 \(\sigma \) 有如下特性，在这个二维空间任何向量 \(\beta \)，都可以分解（投影）为上述两个特征向量方向的向量： \(\beta_1 \,, \beta_2 \)，且有：\(\beta = \beta_1 + \beta_2 \)。那么，则有：\(\sigma(\beta) = \lambda_1 \beta_1 + \lambda_2 \beta_2 \)。即，这个线性变换可以这样描述：先将任何向量沿着特征向量方向分解，然后再按照特征值的大小进行拉伸或压缩，然后再把向量合并起来。

上述的解释，可以对照着右图去理解。特征向量分别为 \((1,1) \) 和 \((-1,1) \) ，即图中浅绿色、浅蓝色方向。该矩阵作用在向量 \((0,1) \) 上，即图中的红色向量。先将红色向量沿着浅绿色、浅蓝色方向分解，然后按照特征值进行拉伸，即图中的绿色、蓝色向量，最后合并为图中的紫色最终向量。

上述的场景是线性变换中，最为简单的一类。而实际的线性变换，则更为复杂，可能还涉及到对于向量的旋转、镜像、剪切等变换。关于更多场景可以自己探索，或者阅读相关书籍，也可以看看这篇文章中的更多直观的例子：特征值与特征向量。

“特征向量”可以很好的帮助理解“方阵”变换，还有一类变换时非方阵的情况，通常这时候可以借助于奇异值分解的方式去理解，关于奇异值分解可以参考：奇异值分解–深度学习的数学基础。

4. 最后

初等的线性代数核心部分大概是这些内容，出于完整性的考虑，可以再进一步了解“Jordan 块”相关的内容，从而把相关理论补充完整，这里不再详述。

如果再回到最初的线性方程组解的问题，我们这里就可以回答最后一个问题：对于一个线性方程组，如果有解，那么所有的解空间是怎样的？

结论：如果方程组的系数矩阵的秩为\( r \)，那么解空间的维度为\( n-r \)。解空间的“基”则可以通过初等变换求得。这里不再详述。