蛇年大吉!
标题:清华大学数据库教授李国良入选 ACM Fellow; 阿里云 PolarDB 打破TPC-C记录
重要更新
清华大学李国良入选ACM Fellow,以表彰其在人机协同(human-in-the-loop)数据集成与基于学习的数据库系统领域做出的重要贡献。此外,李国良还是 openGauss 社区技术委员会主席。[6]
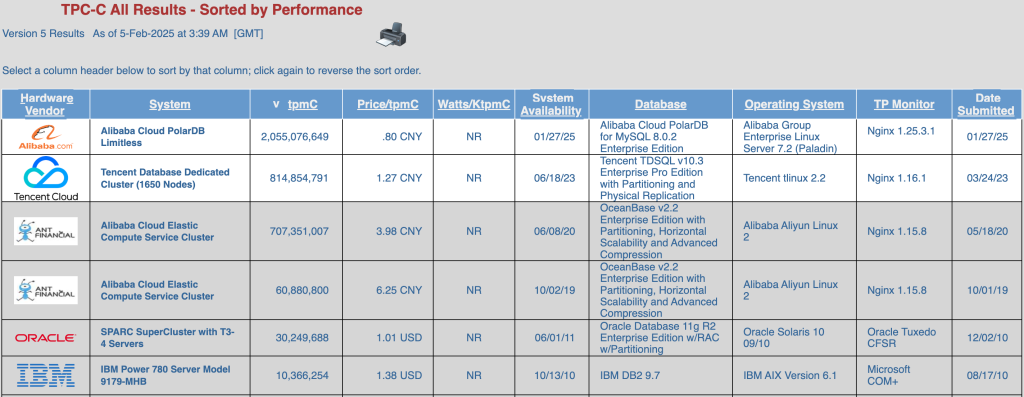
阿里云 PolarDB 打破TPC-C记录[1][2],以更高的性能、更好的性价比超越之前OceanBase、TDSQL创下的记录。PolarDB本次使用的使用的版本为多主集群(Limitless),总计使用2340个数据节点,56,160个cores,1170个处理器[3]。
更新详情
Azure(微软云)
- Azure SQL Database 正式提供免费试用,该试用提供10个数据库、每个32GB的 serverless 实例,每月最多使用资源为100,000 vCore*秒 [5]
GCP(谷歌云)
- Cloud SQL for MySQL 5.6 和 5.7 ,PostgreSQL 9.6、10、11 和 12因为社区生命周期终止 (EOL) ,当前已加入 Cloud SQL 扩展支持阶段 [14][15]
- Spanner 索引顾问在 GoogleSQL 和 PostgreSQL 方言数据库中均已普遍可用。索引顾问会分析您的查询,推荐新索引或对现有索引进行更改,以提高查询的性能[18]
- Spanner 支持新的 SERIAL 和 AUTO_INCREMENT DDL 语法 [19]
- BigQuery ML 支持多项生成式 AI 功能 [27]
- Spanner 支持 GoogleSQL 和 PostgreSQL 方言数据库中的 `SELECT…FOR UPDATE` 查询语法[34]
Oracle云
- HeatWave 支持更改管理员密码 [40]
- HeatWave 支持版本 9.2.0、8.4.4 和 8.0.41 [41]
- OCI 上的 PostgreSQL 数据库增加了对 pg_cron 和 pgaudit 扩展的支持[42]
火山云(字节)
AWS(亚马逊云)
- DocumentDB 现在提供与 CloudShell 的一键连接 [51]
- RDS Custom for SQL Server 使用 io2 Block Express 卷支持高达 64TiB 和 256,000 IOPS [57]
- Timestream for InfluxDb 现已支持存储扩展 [60]
- Aurora PostgreSQL Limitless Database 现在支持 PostgreSQL 16.6 [66]
- ElastiCache 现在支持一键设置 EC2 和缓存之间的连接[68]
参考链接
- [1] https://www.tpc.org/tpcc/results/tpcc_results5.asp?print=false&orderby=tpm&sortby=desc
- [2] https://www.linkedin.com/posts/panfeng-zhou-a16a934_im-excited-to-share-that-weve-just-set-activity-7290434703789109248-7ymy/
- [3] https://www.tpc.org/tpcc/results/tpcc_result_detail5.asp?id=125012701
- [4] https://help.aliyun.com/zh/rds/apsaradb-rds-for-mysql/rds-cluster-edition#section-r7q-mat-pm4
- [5] https://azure.microsoft.com/updates?id=467778
- [6] https://mp.weixin.qq.com/s/-HjfyeW2ucyUWHh_Foah6A
- [14] https://cloud.google.com/sql/docs/mysql/extended-support
- [15] https://cloud.google.com/sql/docs/postgres/extended-support
- [18] https://cloud.google.com/spanner/docs/index-advisor
- [19] https://cloud.google.com/spanner/docs/primary-key-default-value#serial-auto-increment
- [27] https://cloud.google.com//bigquery/docs/reference/standard-sql/bigqueryml-syntax-create-remote-model-open
- [40] https://docs.oracle.com/iaas/releasenotes/mysql-database/heatwave-change-admin-password.htm
- [41] https://docs.oracle.com/iaas/releasenotes/mysql-database/heatwave-920-844-8041.htm
- [42] https://docs.oracle.com/iaas/releasenotes/postgresql/pg_cron-pgaudit.htm
- [45] https://www.volcengine.com/docs/6956/1433810
- [46] https://www.volcengine.com/docs/6956/1111481
- [51] https://aws.amazon.com/about-aws/whats-new/2025/02/amazon-documentdb-one-click-connectivity-cloudshell
- [57] https://aws.amazon.com/about-aws/whats-new/2025/01/amazon-rds-custom-sql-server-iops-io2-block-volumes/
- [60] https://aws.amazon.com/about-aws/whats-new/2025/01/amazon-timestream-influxdb-storage-scaling/
- [61] https://aws.amazon.com/about-aws/whats-new/2025/01/amazon-redshift-enhanced-query-monitoring-dia
- [66] https://aws.amazon.com/about-aws/whats-new/2025/01/amazon-aurora-postgresql-limitless-database-16-6/
- [68] https://aws.amazon.com/about-aws/whats-new/2025/01/amazon-elasticache-1-click-connectivity-setup-ec2-cache