-
标题:Zilliz获Forrester报告全球第一;OB支持向量能力;Azure发布DiskANN,吊打pg_vector;阿里云PG发布内置分析引擎;AWS发布托管Valkey服务
重要更新
Azure发布 PostgreSQL 向量索引扩展
DiskANN,声称在构建HNSW/IVFFlat索引上,速度、精准度都超越pg_vector,并解决了pg_vector长期存在的偶发性返回错误结果的问题 [1] 。阿里云 RDS PostgreSQL 发布AP加速引擎(rds_duckdb)。该引擎提供了列存表和向量化执行能力,显著提升复杂查询的执行速度,且无需修改原始查询语句,从而确保您能够方便且高效地获取结果。当前白名单开放中[7]
OceanBase发布4.3.3版本,支持了向量数据存储与索引功能,这也是4.3版本第一个GA版本[3]。
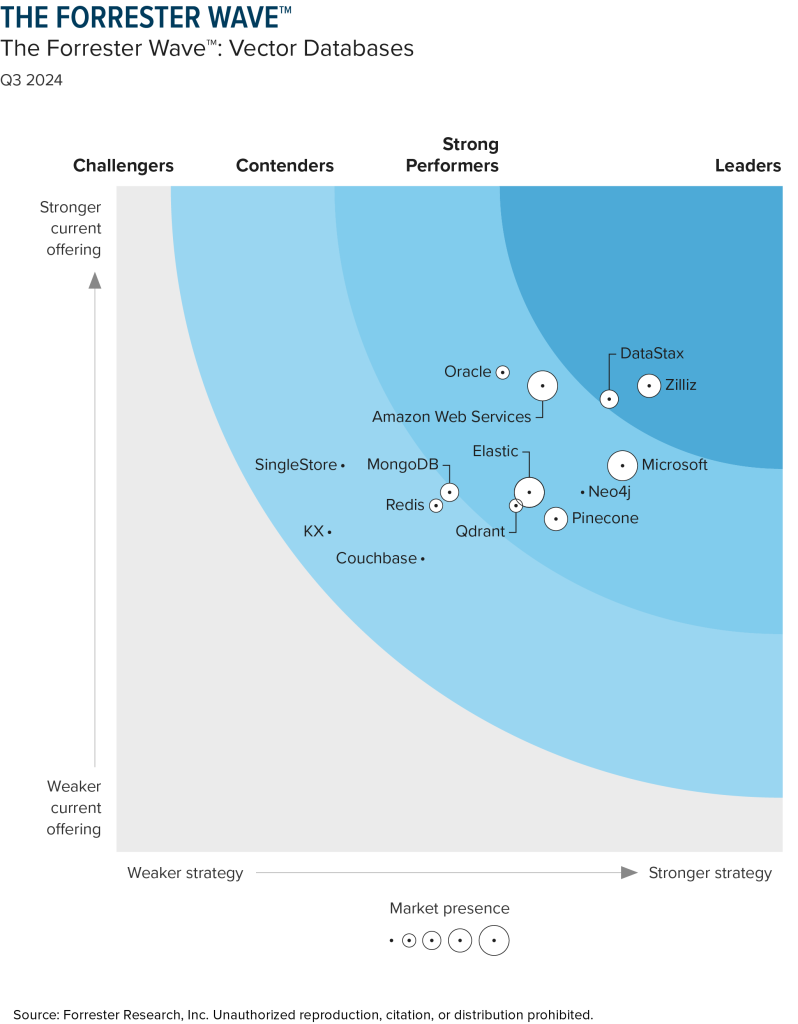
Forrester发布第一份Vector Database的报告(Forrester Wave),Zilliz(产品名:milvus)凭借完整、高效的向量数据处理能力获的第一。后续厂商分别有:DataStax、Microsoft、Amazon、Oracle、Pinecone等[2]。
更新详情
阿里云
- RDS MySQL支持定价详情功能,可以查看各计费项的定价说明和价格。[4]
- RDS PostgreSQL新增支持PostgreSQL 17大版本。[5]
- RDS PostgreSQL高可用系列标准版新增pg.x8.16xlarge.2c(128核 1024GB)独享规格。[6]
- RDS PostgreSQL发布AP加速引擎(rds_duckdb)。该引擎提供了列存表和向量化执行能力,显著提升复杂查询的执行速度[7]
- RDS PostgreSQL 内核版本发布小版本20240830 [8]
- PolarDB Serverless集群支持IMCI列存索引(IMCI)功能 [9]
GCP(谷歌云)
- 创建Cloud SQL支持了证书颁发机构 (CA) 配置功能 [11]
pg_ivm扩展版本 1.9 现已正式发布。此扩展可让您更新物化视图,其中仅计算增量更改并将其应用于视图,而不是从头开始重新计算内容 [12] [13]- “alloydb_scann”扩展程序(以前称为“postgres_scann”)已正式发布(GA),如需详细了解如何存储向量嵌入、创建索引以及调整索引以实现更快的查询性能和更好的召回率,请参阅使用向量。[17]
- 现在,您可以在创建实例后使用“gcloud sql instance patch”命令更新 Cloud SQL for SQL Server 实例的时区。以前,您只能在首次创建实例时为 SQL Server 实例设置自定义时区.[19]
- Cloud SQL for MySQL 8.4 现已正式发布 [24]
- AlloyDB 主实例和备实例上支持公网IP [26]
火山云(字节)
- DBW 数据库审计日志的默认保留时长变更为 30 天,同时新增支持选择保留 180 天、1 年和 3 年。[30]
- 在操作审计页面 DBW 管理员支持查看所有操作行为,DBW 普通用户和非 DBW 系统角色仅支持查看自己的操作行为。[33]
AWS(亚马逊云)
- Aurora Serverless v2 新增支持 256 个 ACU [35]
- Amazon Aurora/RDS 支持控制台到代码 [36]
- Amazon 新增 ElastiCache for Valkey /MemoryDB for Valkey [38] [39]
- Aurora 支持 PostgreSQL 16.4、15.8、14.13、13.16 和 12.20 [50]
- Aurora MySQL 现已支持 RDS 数据 API [51]
腾讯云
- TDSQL-C MySQL 版“只读分析引擎”内核版本更新到1.2404.10.0,主要优化了产品使用的体验和稳定性。支持了 date_sub 函数 [53]
Azure(微软云)
- 托管 PostgreSQL 支持了更多数据库参数的修改 [54]
- 托管 Redis 7.2( Azure Cache for Redis Enterprise)正式发布 [55]
- 托管 PostgreSQL 支持
postgresql_anonymizer插件,更好的保护隐私数据 [56]
参考链接
- [1] https://azure.microsoft.com/en-us/updates/v2/DiskANN-indexing-on-Azure-Database-for-PostgreSQL
- [2] https://mp.weixin.qq.com/s/Sq1GUOTP02QWBOqS0N3A9A
- [3] https://www.oceanbase.com/product/oceanbase-database-rn/releaseNote#V4.3.3
- [4] https://help.aliyun.com/zh/rds/apsaradb-rds-for-mysql/new-features-new-specifications-apsaradb-rds-releases-the-pricing-details-feature
- [5] https://help.aliyun.com/zh/rds/apsaradb-rds-for-postgresql/features-of-apsaradb-rds-for-postgresql
- [6] https://help.aliyun.com/zh/rds/apsaradb-rds-for-postgresql/primary-apsaradb-rds-for-postgresql-instance-types
- [7] https://help.aliyun.com/zh/rds/apsaradb-rds-for-postgresql/use-the-rds-duckdb-extension
- [8] https://help.aliyun.com/zh/rds/apsaradb-rds-for-postgresql/release-notes-for-alipg
- [9] https://help.aliyun.comhttps://help.aliyun.com/zh/polardb/polardb-for-mysql/user-guide/set-the-scale-up-strategy-of-serverless-cluster
- [11] https://cloud.google.com/products#product-launch-stages
- [12] https://cloud.google.com/sql/docs/postgres/extensions
- [13] https://cloud.google.com/sql/docs/postgres/set-maintenance-window
- [17] https://cloud.google.com/alloydb/docs/ai/store-embeddings
- [19] https://cloud.google.com/sql/docs/sqlserver/instance-settings#timezone
- [24] https://cloud.google.com/sql/docs/mysql/create-instance
- [26] https://cloud.google.com/products#product-launch-stages))
- [30] https://www.volcengine.com/docs/6956/155353
- [33] https://www.volcengine.com/docs/6956/1333447
- [35] https://docs.aws.amazon.com/AmazonRDS/latest/AuroraUserGuide/aurora-serverless-v2.how-it-works.html#aurora-serverless-v2.how-it-works.capacity
- [36] https://docs.aws.amazon.com/AmazonRDS/latest/AuroraUserGuide/Using_C2C.html
- [38] https://aws.amazon.com/about-aws/whats-new/2024/10/amazon-elasticache-valkey
- [39] https://aws.amazon.com/about-aws/whats-new/2024/10/amazon-memorydb-valkey
- [50] https://aws.amazon.com/about-aws/whats-new/2024/09/amazon-aurora-supports-postgresql-new-versions/
- [51] https://aws.amazon.com/about-aws/whats-new/2024/09/amazon-aurora-mysql-rds-data-api/
- [52] https://aws.amazon.com/about-aws/whats-new/2024/09/amazon-timestream-for-influxdb-jakarta-milan-uae-zaragoza/
- [53] https://cloud.tencent.com/document/product/1003/109576
- [54] https://azure.microsoft.com/en-us/updates/v2/performance-management-server-parameters-now-modifiable-on-Azure-Database-for-PostgreSQL
- [55] https://azure.microsoft.com/en-us/updates/v2/Redis-7-2-on-Azure-Cache-for-Redis-Enterprise
- [56] https://azure.microsoft.com/en-us/updates/v2/Azure-Database-for-PostgreSQL-support-for-postgresql-anonymizer
-
梯度下降法(或者其改进算法)是机器学习的基础算法之一。在了解梯度下降算法的过程中,会经常看到一句话:“梯度是函数在某一点变化率最大的方向”。本文从较为严格数学证明的角度说明为什么是这样。理解这个证明过程,可以很好的理解梯度下降算法,及其优化算法或者优化方向。
本文主要考虑二元函数场景,即\( z=f(x,y) \)。原因是一元函数场景过于简单,不具有代表性,另外,二元场景向多元场景推广也还比较好理解。
偏导数
偏导数的定义比较好理解,即固定一个变量(当做常数),对另一个变量求导,记作:
$$ \frac{\partial z}{\partial x} \; , \; \frac{\partial z}{\partial y} $$
梯度向量
由各个偏导数组成的向量,就叫梯度向量,通常记作:\( \nabla \),有:
$$ \nabla f = (\frac{\partial z}{\partial x} , \frac{\partial z}{\partial y} ) $$
多元/多维场景,则常记作:
$$ \nabla f = (\frac{\partial f}{\partial x_1} , \frac{\partial f}{\partial x_2} … , \frac{\partial f}{\partial x_n} ) $$
方向导数
多元函数没有简单的“导数”的概念。但为了研究多元函数在某点的变化率,我们可以考虑“方向导数”。
具体的,考虑函数 \( z = f(x,y) \),该函数定义域为\( \mathbb{R}^2 \),其方向向量是 $$ \{ u,v | u^2 +v^2 = 1 \} $$,取其中的一个方向 \( l = (u_0,v_0) \),并假设该方向与\( x \)轴正方向夹角为\( \theta \)。
那么,函数\( z = f(x,y) \)在点\( (x_0,y_0) \)处,在方向 \( l = (u_0,v_0) \)的导数记作
$$ \frac{\partial z}{\partial l} |_{(x_0,y_0)} $$
直观理解方向导数
图1是一个非常清晰的关于方向导数的图例。绿色曲面即为 \( z = f(x,y) \),在点\( A^\prime \)上考虑方向为\( \vec{h}\)的方向导数。过点\( A^\prime \)与方向\( \vec{h}\),与\( z \)轴平行,存在一个平面,即图1中的半透明的平面,该平面与 \( z = f(x,y) \)相交与一条曲线,即图1中的黄色曲线。
那么,该方向导数,即为在该黄色曲线上,\( A^\prime \)位置的导数。这就是关于方向导数的直观理解。
所以,偏导数\( \frac{\partial z}{\partial x} \; , \; \frac{\partial z}{\partial y} \)可以理解为在\( (1,0) \)和\( (0,1) \)这两个方向上的方向导数。
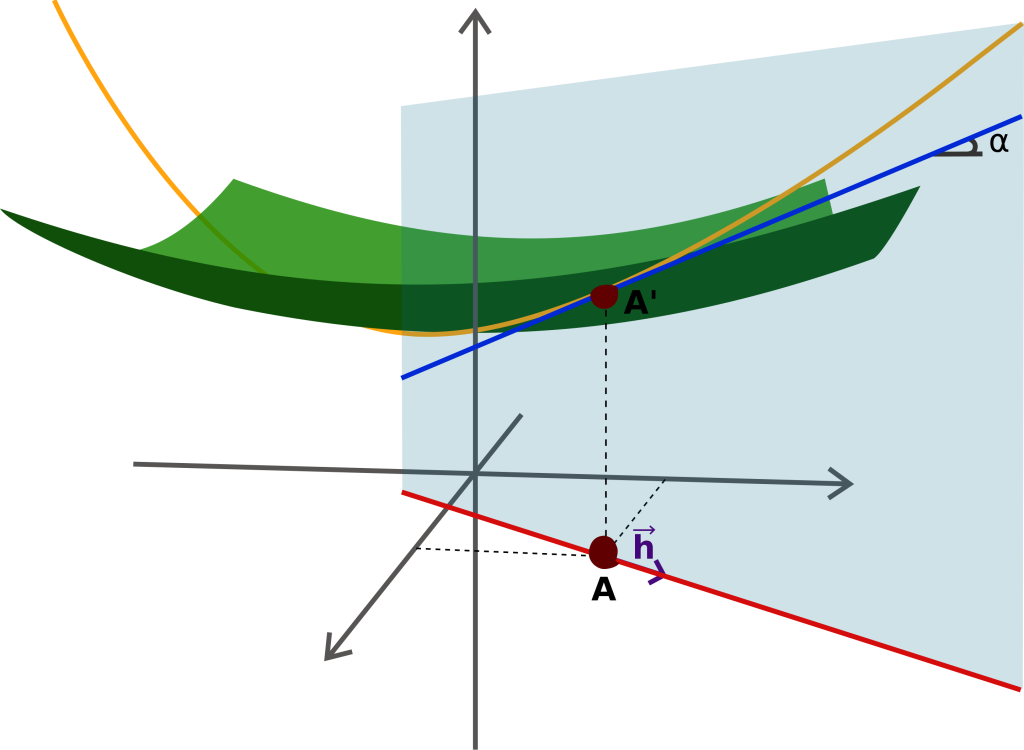
图1:来自Wikipedia: Directional derivative 与一般的导数定义类似的,可以定义方向导数:
$$ \frac{\partial z}{\partial l} |_{(x_0,y_0)} = \lim\limits_{P \to P_0} = \frac{f(P) – f(P_0)}{||P-P_0||} = \lim\limits_{\rho \to 0} \frac{\Delta z}{ \rho } $$
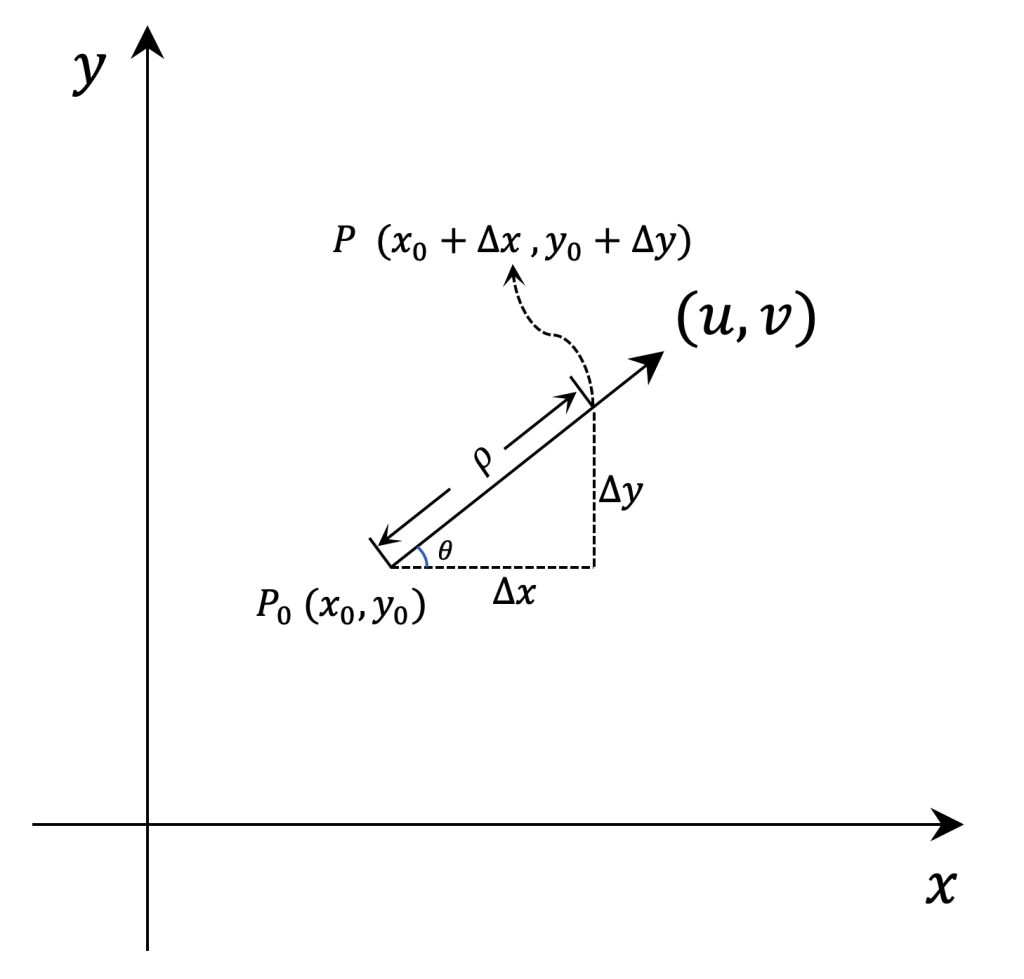
图2:\( P \) 点在\( (u,v) \)方向逼近\( P_0 \) 可以到如下结论(详细证明参考后续小节“方向导数的计算与证明”),如果方向\( l = (u_0,v_0) \)与 \( x \)轴的夹角是\( \theta \),那么\( z = f(x,y) \)在点\( (x_0,y_0) \)处,在方向 \( l = (u_0,v_0) \)的导数取值如下:
$$ \frac{\partial z}{\partial l} |_{(x_0,y_0)} = \frac{\partial z}{\partial x} |_{(x_0,y_0)} cos(\theta) + \frac{\partial z}{\partial y} |_{(x_0,y_0)} sin(\theta) \tag{1} $$
根据柯西不等式,我们有如下结论:
$$ \frac{\partial z}{\partial l} |_{(x_0,y_0)} = \frac{\partial z}{\partial x} |_{(x_0,y_0)} cos(\theta) + \frac{\partial z}{\partial y} |_{(x_0,y_0)} sin(\theta)
\\
\le \sqrt{ ((\frac{\partial z}{\partial x} |_{(x_0,y_0)})^2 + (\frac{\partial z}{\partial y} |_{(x_0,y_0)})^2)(sin^2(\theta)+cos^2(\theta)) }
\\
= \sqrt{ (\frac{\partial z}{\partial x} |_{(x_0,y_0)})^2 + (\frac{\partial z}{\partial y} |_{(x_0,y_0)})^2 }
$$上面表示的极值 \( \sqrt{ (\frac{\partial z}{\partial x} |_{(x_0,y_0)})^2 + (\frac{\partial z}{\partial y} |_{(x_0,y_0)})^2 } \) 正是偏导数向量的“范数”(长度),根据柯西不等式取最大值的条件也有:
$$
\frac{cos(\theta)}{\frac{\partial z}{\partial x}} = \frac{sin(\theta)}{\frac{\partial z}{\partial y}}
\\
tan(\theta) = \frac{\frac{\partial z}{\partial y} } { \frac{\partial z}{\partial x} } = \frac{\Delta y}{\Delta x}
$$所以,即,即当方向恰好为偏导数向量时,方向导数取最大值。也就是,我们经常会说的,会看到的,“偏导数向量是所有方向中最为陡峭的方向”或者说“梯度是函数在某一点变化率最大的方向”。
方向导数的计算与证明
在前面,我们是直接给出了如下的结论的:
$$ \frac{\partial z}{\partial l} |_{(x_0,y_0)} = \frac{\partial z}{\partial x} |_{(x_0,y_0)} sin(\theta) + \frac{\partial z}{\partial y} |_{(x_0,y_0)} cos(\theta)$$
这个结论的获得,是需要有一些比较复杂的计算或者说证明的。这里,其主要证明步骤/方法之一,如下:
\( \frac{\partial z}{\partial l} |_{(x_0,y_0)} = \lim\limits_{P->P_0}\frac{f(P)-f(P_0)}{|P-P_0|} = \lim\limits_{P->P_0}\frac{f(x_0+\Delta{x},y_0+\Delta{y})-f(x_0,y_0)}{\sqrt{\Delta{x}^2+\Delta{y}^2}}
\)由拉格朗日中值定理:存在\( \alpha \; \beta \),使得下式成立,且 \( 0 \le \alpha \le 1 \; and \; 0 \le \beta \le 1 \):
\(
f(x_0+\Delta{x},y_0+\Delta{y})-f(x_0,y_0)
\\
= [f(x_0+\Delta{x},y_0+\Delta{y}) – f(x_0,y_0+\Delta{y})] + [f(x_0,y_0+\Delta{y}) -f(x_0,y_0)]
\\
= f_x'(x_0 + \alpha\Delta{x} ,y_0+\Delta{y})\Delta{x} + f_y'(x_0, y_0 + \beta\Delta{y} )\Delta{y}
\)容易有,这几个条件是等价的: \( P \to P_0 \)、\( \Delta{x} \to 0 \, and \, \Delta{y} \to 0 \) 、\( \sqrt{\Delta{x}^2+\Delta{y}^2} \to 0 \)
考虑\( \frac{\partial z}{\partial x} \)在\( (x_0,y_0)\)处连续(这是一个条件),则有: $$ \lim\limits_{\Delta{x} \to 0 \\ \Delta {y} \to 0 }f_x'(x_0 + \alpha\Delta{x} ,y_0+\Delta{y}) = f_x'(x_0,y_0) $$
故:
$$
\begin{align}
\frac{\partial z}{\partial l} |_{(x_0,y_0)} & = \lim\limits_{P->P_0}\frac{f(P)-f(P_0)}{|P-P_0|}
\\
& = \lim\limits_{P->P_0}\frac{f(x_0+\Delta{x},y_0+\Delta{y})-f(x_0,y_0)}{\sqrt{\Delta{x}^2+\Delta{y}^2}}
\\
& =\lim\limits_{P->P_0}\frac{f_x'(x_0+\alpha\Delta{x},y_0+\Delta{y})\Delta{x} + f_y'(x_0,y_0+\Delta{y})\Delta{y}}{\sqrt{\Delta{x}^2+\Delta{y}^2}}
\\
& =\lim\limits_{P->P_0}\frac{f_x'(x_0+\alpha\Delta{x},y_0+\Delta{y})\Delta{x}}{\sqrt{\Delta{x}^2+\Delta{y}^2}} + \frac{f_y'(x_0,y_0+\Delta{y})\Delta{y}}{\sqrt{\Delta{x}^2+\Delta{y}^2}}
\end{align}
$$根据上面的图2,容易有:
$$
\frac{\Delta{x}}{\sqrt{\Delta{x}^2+\Delta{y}^2}} = cos(\theta) \quad \frac{\Delta{y}}{\sqrt{\Delta{x}^2+\Delta{y}^2}} = sin(\theta)
$$所以:
\( =\lim\limits_{P->P_0}\frac{f_x'(x_0+\alpha\Delta{x},y_0+\Delta{y})\Delta{x}}{\sqrt{\Delta{x}^2+\Delta{y}^2}} + \frac{f_y'(x_0,y_0+\Delta{y})\Delta{y}}{\sqrt{\Delta{x}^2+\Delta{y}^2}}
\\
=f_x'(x_0,y_0)cos(\theta) + f_y'(x_0,y_0)sin(\theta)
\\
\)好了,这就证明完成了。
关于上述证明
上述证明,在一般的《数学分析》教程的“多元函数微分”相关章节都会有,或者会有类似的问题证明。过程还是比较巧妙的,先是“无中生有”新增了一个项(\( f(x_0,y_0+\Delta{y}) \)),分别构造了关于 \( x \)和\( y \)的偏导数,然后使用了“中值定理”,将差值变成,导数和微分变量的积(准确的说,还要加上一个关于\( \rho \)的高阶无穷小)。
向量形式化表达
使用向量形式化表达,看起来会简洁很多。对于方向向量(这也是一个单位向量) \( \mathbf{l} = (u,v)\),函数\( f \)的偏导数向量记为\( \nabla f = (\frac{\partial z}{\partial x} , \frac{\partial z}{\partial y} ) \) ,那么方向导数为 \( D_{\mathbf{l}}f(P_0) = \nabla f \cdot \mathbf{l} \) ,这与上面表达式的意义是相同的。
根据点击的性质,我们有:
\( D_{\mathbf{l}}f(P_0) = \nabla f \cdot \mathbf{l} = ||\nabla f|| ||\mathbf{l} || cos\theta = ||\nabla f|| cos\theta \)
从这里,更容易看出,方向向量与梯度向量相同时,方向导数取最大值,最大值即为梯度向量的模。
多维场景扩展
在很多的材料中,在前面的表达式中,经常会看到的是 \( cos(\alpha) \; cos(\beta) \),而不是本文中的 \( sin(\theta) \; cos(\theta) \)。这里的 \( \alpha \)是方向向量与x轴正方向的夹角, \( \beta \)是方向向量与y轴正方向的夹角;在定义域 \( \mathbb{R}^2 \)上有:\( \alpha + \beta = 90^{\circ} \),即有 \( cos^2\alpha + cos^2\beta = 1 \)。
这种写法有着更好的扩展性,当在更多元的情况下,例如三元场景下,即 \( z = f(x_1,x_2,x_3) \),方向向量与 x,y,z轴的夹角分别是:\( \alpha \; \beta \; \gamma \),则有: \( cos^2\alpha + cos^2\beta + cos^2 \gamma = 1 \)。
任意维度,也有类似的结论,并且应用柯西不等式时,上述结论也是类似的。
说明:直觉
本文内容需要或者可以建立如下的“直觉”:
- 在一维空间(即\( \mathbb{R}\)上的函数,在某一点上的一阶导数的符号(正/负),可以代表在该方向上,函数的趋势是增长还是下降,“正号”,则是增长;“负号”,则是下降。
- 在一维空间(即\( \mathbb{R}\)上的函数,在某一点上的一阶导数的绝对值大小,即为其“陡峭程度”(更多的时候理解为,变化率大小)
上述两个结论,基本上认为是显然的。下面扩展到多维场景,也几乎是显然的:
- 在高维空间/多维变量(即\( \mathbb{R}^n\)时,在某一点的任意方向上,都有导数,称为方向导数,该方向导数的符号(正/负),可以代表在该方向上,函数的趋势是增长还是下降,“正号”,则是增长;“负号”,则是下降。
- 在高维空间/多维变量(即\( \mathbb{R}^n\)时,在某一点的任意方向上,都有导数,该导数的绝对值大小,即为其“陡峭程度”(更多的时候理解为,变化率大小)
- 更进一步的,也就是本文中的一个结论:高维空间/多维变量(即\( \mathbb{R}^n\)时,函数的所有的方向导数,在偏导数向量方向上,取值最大,即是最为“陡峭”的方向。
所以,最后
所以,这就是为什么梯度下降算法中,总是倾向于选择偏导数向量方向进行下一次迭代。
在本科毕业后,最后留了几本书:《数学分析》(上下册)、概率论,一直到研究生毕业、再到工作都一直带着,还从北京邮寄到了杭州。本想只是做个纪念的,没想到竟然还能用上…
-

CentOS 7/8目前已经不再更新,如果不打算使用CentOS Stream、RHEL的话,最主要的选择是AlmaLinux和Rocky Linux。对于一般的开发者来说,两者并没有太大区别,使用体验都100%兼容RHEL,也与原来的CentOS几乎相同。从其他方面,这里来对比一下AlmaLinux和Rocky Linux。
生态情况
双方都声称自己的生态非常好,不看广告看疗效,这里通过对比主要云厂商对于这两个发行版的支持来粗略判断其生态情况。统计数据如下:
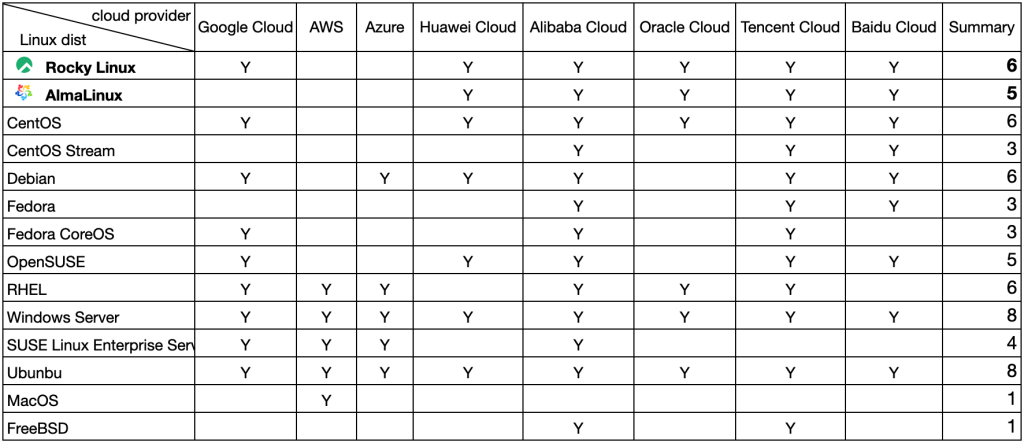
数据参考:Linux Dist. on Cloud by default 从数据上看,Rocky Linux略胜一筹(6分 VS 5分)。也顺便统计了,所有的Linux发行版在各个云的默认支持情况,其他几个值得关注的发行版包括:Ubuntu(8分)、RHEL(6分)、Debian(6分)、SUSE(5分)。
详细的云厂商支持情况截图如下,该数据根据各个云厂商在ECS/VM/EC2的创建过程中,可以手动选择的、非云市场的Linux发型版本:

阿里云 
AWS 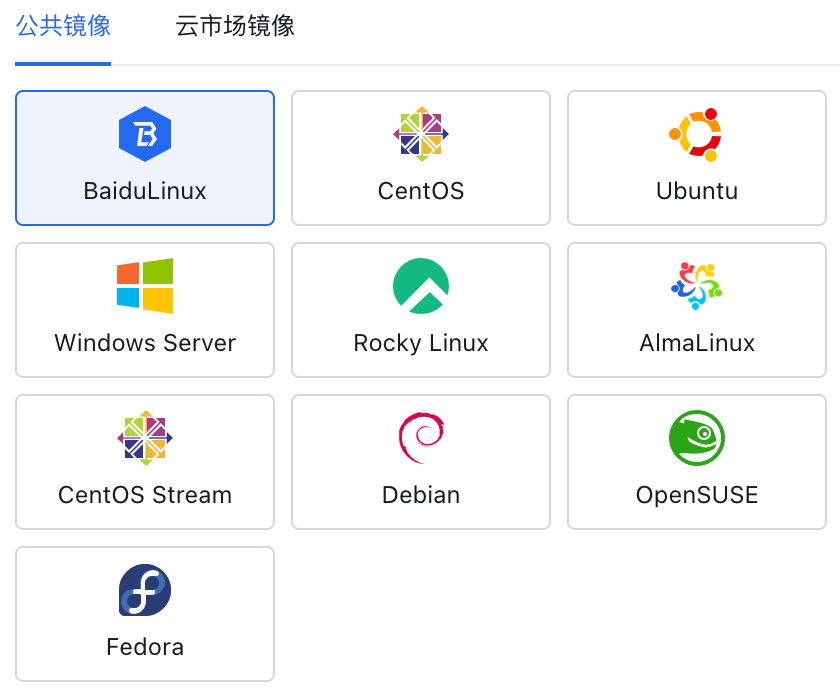
百度云 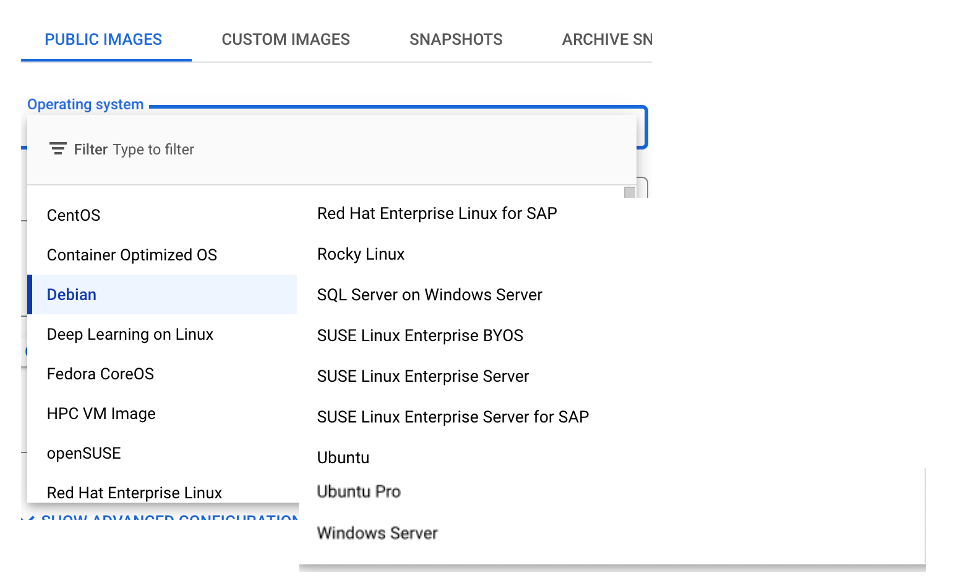
Google Cloud 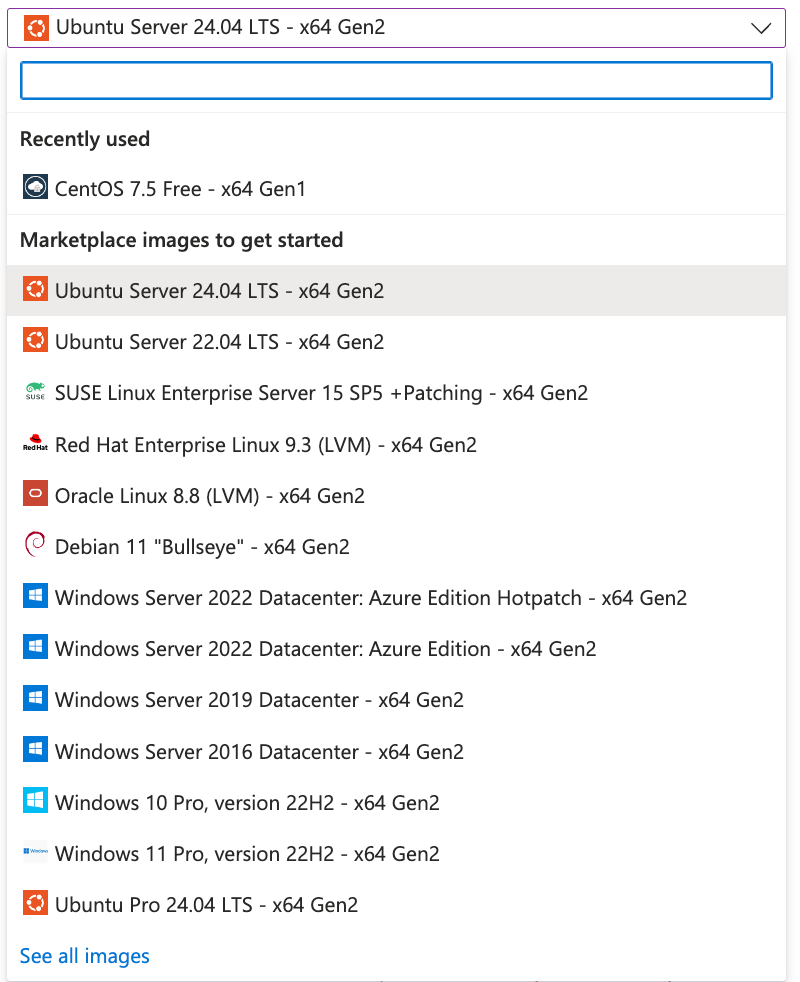
Azure 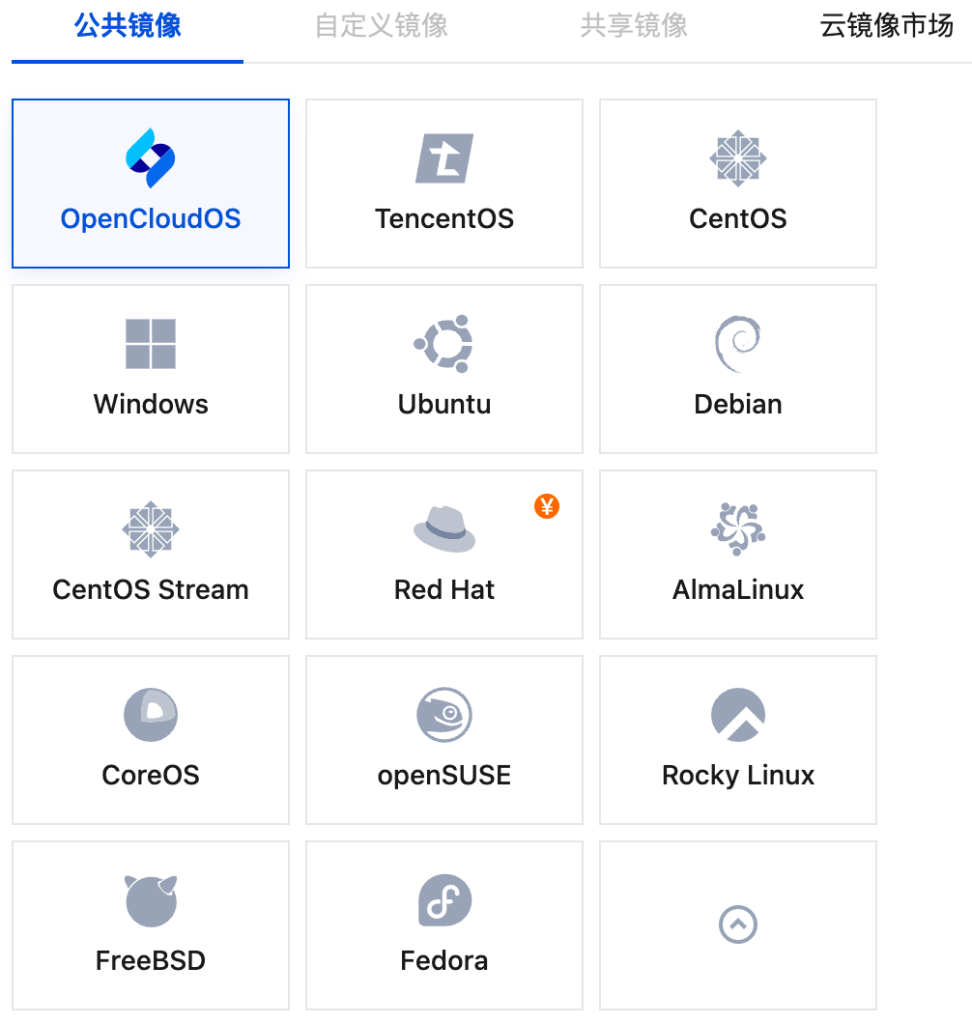
腾讯云 
Oracle Cloud 
华为云 这里给出的列表为云厂商在“默认推荐”中的发行版,例如,在AWS中被认为是 Commonly Used AMI、Azure上则是表现为在其镜像直接的选择列表中。列表中不包含,各个云厂商的自己的发行版,包括Amazon Linux、Alibaba Cloud Linux、Anolis OS、Oracle Linux、TencentOS、Baidu Linux等。
Google Trend数据
Google Trend也是非常好的代表流行度的指标,具体数据参考右图。可以看到,两个发行版都有不错的增长趋势,Rocky Linux则再次略胜一筹。
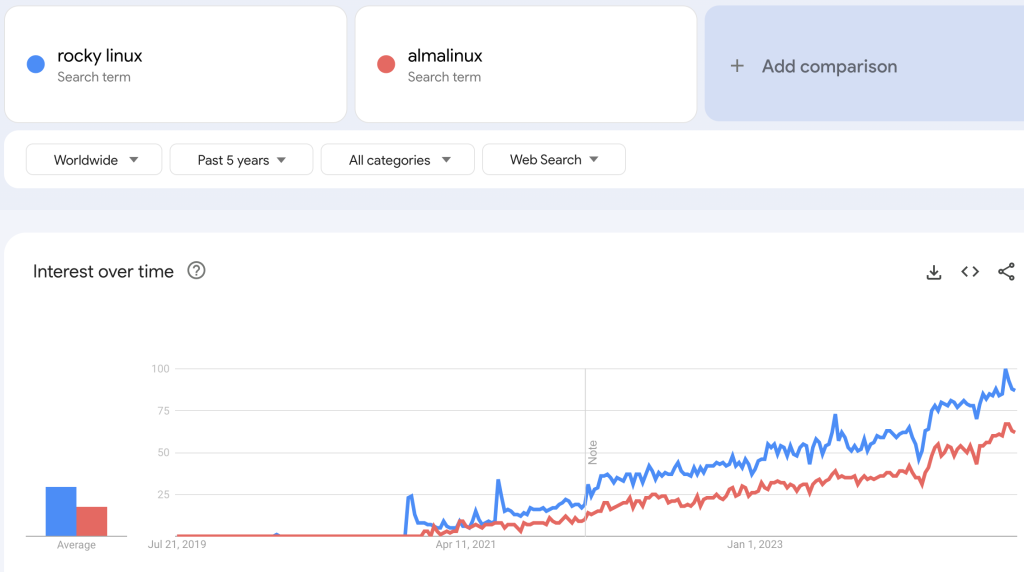
此外,如果是非RHEL兼容的版本,那么Debian也是不错的选择。
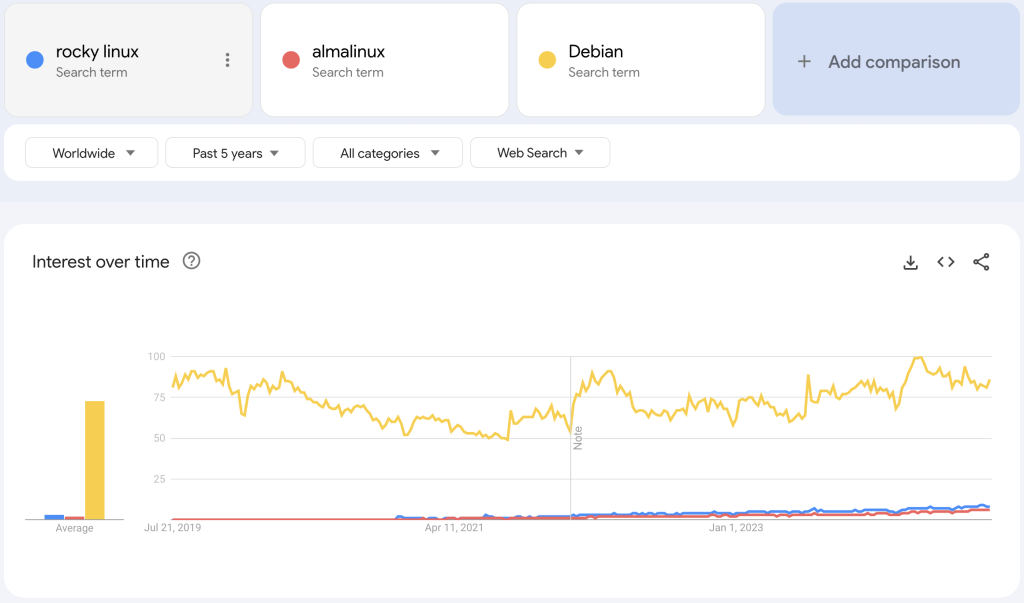
基金会架构
AlmaLinux背后是Alma Linux基金会,这是一个非盈利机构(501(c)(6)),该机构最初由Cloudlinux(是一家商业公司)赞助,并还在持续赞助。相对来说,AlmaLinux有一定的独立性。
Rocky Linux是由CentOS创始人创办,而且使用类似的架构。Rocky Linux依旧是以社区的形式运作,但是其商标、和其基金会是由商业公司拥有。
官网
小结
最后,生态现状和受关注度上Rocky Linux更胜一筹;在公司架构上,AlmaLinux是一个最初由Cloudlinux资助建立的非盈利组织,Rocky Linux架构则与之前的CentOS类似由商业公司驱动。AlmaLinux、Rocky Linux两者就像“麦当劳”和“肯德基”,有人说麦当劳的鸡翅好吃,有人说肯德基的鸡米花好吃,也有很多人是尝不出来两者的区别的,根据偏好选择就好了。
笔者给一个非常玄乎的建议,如果你的偏好是麦当劳,建议使用AlmaLinux,如果是KFC则建议Rocky Linux。如果你也无所谓,那么关于这两个选择也就无所谓,“点兵点将骑马打仗”就好了。
参考:
- https://wiki.almalinux.org/Comparison.html
- https://www.reddit.com/r/AlmaLinux/comments/13050fo/why_almalinux_instead_of_rocky_linux/
-
标题:李飞飞发布Data+AI多模平台; Supabase完成C轮8000万美元融资; OceanBase将上线阿里云精选市场重要更新
云栖大会阿里云李飞飞发布由Data+AI驱动的多模数据管理平台DMS:OneMeta+OneOps、DMS+X、PolarDB Always On、Tair Serverless KV、ADB软硬件加速/AI智能分析等产品与能力 [3]
OceanBase Cloud 两周年线上见面会,总结两年来的创新与突破。OB将通过TP/AP 一体化、多模一体化、多云原生等能力帮助企业降本提效。同时宣布了OB Cloud将作为独立的数据库厂商,登陆阿里云精选市场 [28] 。
Supabase 完成C轮8000万美元融资,该平台以PostgreSQL为中心,向开发者提供各类服务的平台,包括数据库、认证服务、存储、实时事件同步、向量数据库等 [1] [2]
更新详情
阿里云
- RDS PostgreSQL支持基础系列或高可用系列升级为集群系列。[4]
Azure
- Azure Data Studio (ADS)上的PostgreSQL迁移插件将于11月15退休,不再进行维护与支持 [12]
- Cosmos DB 支持按地区、按分配进行扩缩容 [7]
- Azure Database for PostgreSQL支持在线的从Single Server到Flexible Server [8]
- Azure Database for PostgreSQL 支持新的小版本16.4, 15.8, 14.13, 13.16, 12.20, and 17 Beta 3 [9]
火山云(字节)
- DBW 控制台支持查看云数据库 PostgreSQL 的会话统计和实时会话等信息。[10]
AWS(亚马逊云)
- RDS for Oracle 支持 Oracle Management Agent 13.5.0.0.v2 [13]
- RDS Performance Insights 支持 Aurora 集群级配置 [22]
腾讯云
- 云数据库 PostgreSQL 在15版本支持 pglogical 插件的标准化使用。[24]
- 云数据库 PostgreSQL 14、15、16支持 SQL 限流能力,可以基于 query_id 和 SQL 语句进行限流设置。[25]
- 云数据库 PostgreSQL 13的云数据库 PostgreSQL 实例支持通过插件 starocks_fdw 实现冷热数据分离。[26]
- 云数据库 PostgreSQL 支持在控制台进行 database 对象的管理。[27]
GCP(谷歌云)
- GCP DMS 支持从 SQL Server 迁移到 Cloud SQL for SQL Server [5]
- GCP DMS 支持从 PostgreSQL 迁移到 AlloyDB for PostgreSQL 16 [6]
参考链接
- [1] https://techcrunch.com/2024/09/25/supabase-a-postgres-centric-developer-platform-raises-80m-series-c/
- [2] https://supabase.com/
- [3] https://mp.weixin.qq.com/s/igmMR0CFLZXjKjuA4bZ-lA
- [4] https://help.aliyun.com/zh/rds/apsaradb-rds-for-postgresql/upgrade-the-rds-edition-from-rds-basic-edition-or-rds-high-availability-edition-to-rds-cluster-edition
- [5] https://cloud.google.com/database-migration/docs/sqlserver/scenario-overview
- [6] https://cloud.google.com/database-migration/docs/postgresql-to-alloydb/migration-src-and-dest
- [7] https://azure.microsoft.com/en-us/updates/v2/Azure-Cosmos-DB-dynamic-scaling
- [8] https://azure.microsoft.com/en-us/updates/v2/Online-migration-from-Azure-Database-for-PostgreSQL-Single-Server-to-Flexible-Server
- [9] https://azure.microsoft.com/en-us/updates/v2/Latest-PostgreSQL-minor-versions-supported-by-Azure-Database-for-PostgreSQL
- [10] https://www.volcengine.com/docs/6956/1340582
- [11] https://www.volcengine.com/docs/6956/1340585
- [12] https://azure.microsoft.com/en-us/updates/v2/Azure-PostgreSQL-migration-extension-in-Azure-Data-Studio-1
- [22] https://aws.amazon.com/about-aws/whats-new/2024/09/amazon-rds-performance-insights-supports-aurora-cluster-level-configuration
- [23] https://aws.amazon.com/about-aws/whats-new/2024/09/aws-database-migration-service-enhanced-monitoring/
- [24] https://cloud.tencent.com/document/product/409/111199
- [25] https://cloud.tencent.com/document/product/409/111196
- [26] https://cloud.tencent.com/document/product/409/111197
- [27] https://cloud.tencent.com/document/product/409/111024
- [28] https://mp.weixin.qq.com/s/_MPJf9BOaK_2cV5jz__0qg
-
本文是一个系列文章的一部分,该系列较为完整的对各个云厂商的RDS MySQL进行了测试,包括了阿里云、腾讯云、华为云、百度云、AWS、Azure、GCP、Oracle Cloud等,最新的测试:云数据库RDS MySQL的性能。
在不同的云厂商,购买相同规格的MySQL实例(如4vCPU-16GB),获得的性能相同吗?
data aliyun_202409_hangzhou->stdbench tencent_202409_beijing_exclusive->stdbench hwcloud_202409_beijing_x86->stdbench baiducloud_202409_beijing->stdbench aws_202409_tokyo_m6i->stdbench azure_202409_east_asia_4c16g->stdbench gcp_202409_tokyo_80_enterprise->stdbench oci_202409_tokyo_8039->mysql_on_4_ecpu 4 7102 5592 2557 2206 1639 2025 723 3551 8 9702 9936 4674 4101 3313 3654 1341 5936 16 14660 16141 8229 7298 6427 6548 2502 8054 32 22155 22336 13520 12022 12157 10363 4857 8317 48 27905 24770 17849 16448 16516 11973 6745 8130 64 32704 26495 20114 18187 18118 12761 8071 7838 96 36846 29077 20883 21007 20782 13300 9675 8504 128 39697 29918 20128 21029 22446 13388 10620 8198 192 38999 30610 20521 22091 22590 13478 11507 8043 256 38356 31052 21187 21665 22323 12985 11872 7907 384 39679 31224 21729 21167 21902 12904 12131 8209 512 40333 31805 22647 21627 21591 12930 12106 8386 cpu_capacity 80.4 93.3 163.6 73.9 110.9 56.3 49.9 114.7 测试结果概述
在本次测试中:阿里云RDS MySQL性能表现最好,极限的QPS达到了4万;其次是腾讯云,达到了3.2万;第二梯队是华为云、百度云和AWS,极限的QPS约2.2万;之后是Azure、Google云,极限QPS约1.2万;最后是Oracle云,极限QPS约8500。详细的数据和趋势图,可以参考以上的图、表,这里不再详述。
(more…)